Question 984499: There are two solutions for x to the equation
a|x + b| + c = 0
To 2 decimal places, what is the value of the greater of the two solutions when a = 22, b = 12 and c = -11?
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source):
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Instead of doing your problem for you, I'll do another one that is just
exactly in every detail and step like yours. Sop you can use it as a
model to go by. I'll do this one instead:
a|x + b| + c = 0
To 2 decimal places, what is the value of the greater of the two solutions when a = 12, b = 10 and c = -8?
12|x + 10| + (-8) = 0
12|x + 10| = 8
Divide both sides by 4
3|x + 10| = 2
Since what's inside the absolute value can be either positive
or negative, we make two equations, one where x + 10 is positive
and one where x + 10 is negative.
3[+(x + 10)] = 2 or 3[-(x + 10)] = 2
3x + 30 = 2 or -3x - 30 = 2
3x = -28 or -3x = 32
x =  or x = 
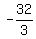x = -9.33 x = -10.67
The greater of those two solutions, since they are both negative,
is the one that's the least far below zero, and -9.23 is not
as far below zero as -10.67.
So the answer is -9.33
Now do your problem exactly the same way, step by step.
Edwin
|
|
|
