Question 976058: let a function f be defined by
f(x) = x^2-2x-3/x^2+2x+3
i) determine the domain of f(x)
ii) find the range of f(x)
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
You can put this solution on YOUR website! Like this:
f(x) = (x^2-2x-3)/(x^2+2x+3)
Which will properly render as  . .
Factor as much as possible.
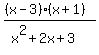
Only two critical x values. Denominator is positive everywhere and has no real roots, so no
vertical asymptotes. Numerator gives f(x) its roots, which are 3 and -1. The numerator is
equivalent itself to a parabola, and in this example, f is negative between the roots and positive
outside the interval which the roots bind.
Domain: All real numbers.
The function f(x) is not a parabola. There is a minimum, and a horizontal asymptote. (Degree is two
for both numerator and denominator).

Only two critical x values. Denominator is positive everywhere and has no real roots, so no
vertical asymptotes. Numerator gives f(x) its roots, which are 3 and -1. The numerator is
equivalent itself to a parabola, and in this example, f is negative between the roots and positive
outside the interval which the roots bind.
Domain: All real numbers.
The function f(x) is not a parabola. There is a minimum, and a horizontal asymptote. (Degree is two
for both numerator and denominator).

|
|
|