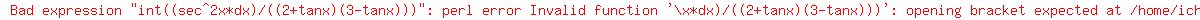[Your hint says to use t = tanx, but most teachers and books use
the letter u rather than the letter t, so I'll use u = tanx, but
you can substitute t everywhere I have u if you like.]
let 
, then 
, 
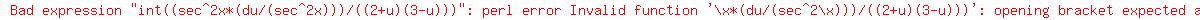
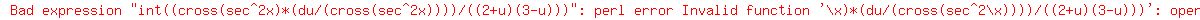
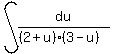Break 
into partial fractions:
But before doing that let's get the denominators in descending
powers of u.
[That isn't absolutely necessary but it is customary because it
keeps things more orderly. Also it is customary to get the
leading term positive, which I will do on the second term]
2+u = u+2 <--first term, just turn it around
3-u = -u+3 = -(u-3) <--second term, factor out -1
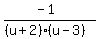
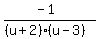
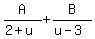
This has to be identically true for all u so substitute u=3
to make the first term on the right become 0
substitute u=-2 to make the second term on the right become 0:
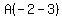
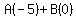
So our integral is now
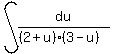
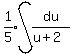
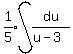
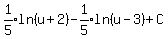
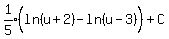
Substitute
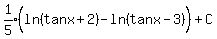Edwin
