SOLUTION: The number of homes in our town with a broadband internet connection has been growing rapidly, as recorded in these points: (0, 3681), (1, 5888), (2, 9422), where the first coordi

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: The number of homes in our town with a broadband internet connection has been growing rapidly, as recorded in these points: (0, 3681), (1, 5888), (2, 9422), where the first coordi      Log On


   

Question 768178: The number of homes in our town with a broadband internet connection has been growing rapidly, as recorded in these points: (0, 3681), (1, 5888), (2, 9422), where the first coordinate is years after we begin to collect data and the second coordinate is the number of wired homes. Develop an exponential model for this scenario, with a base accurate to 2 decimals, then use your model to predict the count for year 4.
Homes with broadband in year 4 (nearest integer, no comma):
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Assume the exponential model has the form:

y = a·eb·x

Substituting (x,y) = (0,3681),

3681 = a·eb·0

3681 = a·(1)

3681 = a

So we now know a, and can write:

y = 3681·eb·x

Substituting (x,y) = (1,5888),

5888 = 3681·eb·1

5888%2F3681 = eb

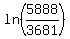b = ln%285888%2F3681%29

b = 0.469731927

Substituting (x,y) = (2,9422),

5888 = 3681·eb·2

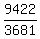9422%2F3681 = eb

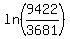2b = ln%289422%2F3681%29

2b = 0.9398629259

 b = 0.4699314629

Both values of b round off the b = 0.470

So we will use 0.470 for b, and the formula

y = 3681·eb·x

becomes:

y = 3681·e0.470x

Now we substitute x=4

y = 3681·e0.470·4

y = 3681·e1.88

y = 24123.4514

Rounded to the nearest whole number,

y = 24123

Edwin