Question 383934: I have an equation -36wx^2-114wx-70w that needs to be factored completely, i get to 2w(-18x^2-57x-35) but then am not able to simplify it any more, and was just curious if thats the final result?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!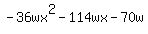 
There is nothing wrong about factoring out 2w and getting:
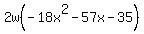
But as you see, the squared term has a negative coefficient. This makes subsequent factoring a little more difficult. So in situations like this I prefer to factor out the negative of the GCF, -2w, giving us:
Next we try to factor 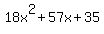 . This is a trinomial which does not fit any of the factoring patterns. Factoring this trinomial usually involves trial and error of different possible factors until you find the one (and there is only one) that works. Using the factors of 18 and 35, we will try combinations until we find the right one that results in 57x in the middle. Here is a list of just some of the possible combinations to check.
(18x+35)(x+1)
(18x+1)(x+35)
(9x-1)(x-35)
(6x+5)(3x+7)
etc.
For 18 the factors are 1*18, 2*9 and 3*6. For 35 the factors are 35*1 and 7*5. The total number of combinations is: 3*2*2*2 = 24. (3 for 3 pairs of factors of 18, 2 for two pairs of factors of 35, 2 to include the negative factors and the last 2 for swapping the order [(18x+35)(x+1) and (18x+1)(x+35) are different and count as two of the combinations.]
With 24 possible combinations is can take a while to find the right one, if it exists! After all, this trinomial may not factor!
For expressions like this where there is a significant number of possible combinations here's a "trick" you can use. (It's totally valid Math, not some magic your teacher would not like to see you use.) It involves using the Quadratic Formula is a way you may have not seen before.
The Quadratic Formula:
The part of the formula inside the square root,  , is called the discriminant. It can be used to predict the number and types of solutions to a quadratic equation. In factoring we can use it in a different way. We can use it to figure out if the quadratic trinomial will factor. Finding out at the start that the trinomial will not factor will save us a lot of time trying combinations which are doomed to fail.
If the value of the discriminant is a perfect square the trinomial will factor. If the value of the discriminant is a not perfect square the trinomial will not factor. Let's try this on your quadratic expression. Your "b" is 57, "a" is 18, and "c" is 35:
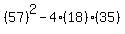
which simplifies as follows:
3249 - 4(18)(35)
3249 - 2520
729
Your discriminant is 729. 729 is a perfect square ( ). So we now now that
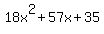will factor. So trying the combinations is not a total waste of time.
We can also use the Quadratic Formula to find the right combination!
In long form this is:
 or 
These simplify:
 or 
 or 
This makes the factors:
(6x - (-5))(3x - (-7))
Note that the factors will have a minus in the middle and note where the numerator and denominator of each fraction goes. These factors simplify to
(6x + 5)(3x + 7)
This makes our final answer:
So we can factor trinomials by any of the following methods:- Try all the different combinations, not knowing if any of them will work, until you find the one that works or you run out of combinations. This can be time-consuming and if you happen to overlook the right combination you may incorrectly decide that the trinomial will not factor.
- Find the discriminant and if it is a prefect square we can either:
- Try the different combinations knowing that one of them will work! So if you can't find the right combination then you must be overlooking the right one. Or
- Use the whole quadratic formula, as I've shown above, to find the actual factors. (Note: If the discriminant is zero then you end up with two identical factors.)
If the discriminant is not a perfect square (and remember that negative numbers cannot be perfect squares), then you know that the trinomial will not factor.
When I factor trinomials, the number of combinations determines which approach I use. If the number of combinations is fairly low or if the right combination is "obvious" to me then I use the first approach. Otherwise I use the discriminant to determine if it is worth continuing.
In summary, you don't have to learn how to use the Quadratic Formula to factor. But it can save you a lot of time when there are a significant number of combinations to try.
|
|
|
