Question 253889: beryllium-11 decomposes into boron-11 with a half life of 13.8 seconds. How long will it take 240 g of beryllium-11 to decompose into 7.5g of beryllium-11?
based on the forumula provided in the text book C(t)=C(0)2e^-t/h
where C(0) = 240, C(t)=7.5 ,h=13.8
7.5/240=2e^-t/13.8
this was a s far as i got
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! beryllium-11 decomposes into boron-11 with a half life of 13.8 seconds. How long will it take 240 g of beryllium-11 to decompose into 7.5g of beryllium-11?
based on the forumula provided in the text book C(t)=C(0)2e^-t/h
where C(0) = 240, C(t)=7.5 ,h=13.8
7.5/240=2e^-t/13.8
this was a s far as i got
------------------------------------
7.5/240=2e^(-t/13.8)
---
(7.5/480) = e^(-t/13.8)
Take the natural log of both sides to get:
-t/13.8 = -4.1589
t = 57.39 seconds
=====================
2nd attempt using a standard half-life formula:
A(t) = A(0)(1/2)^(t/h)
7.5 = 240*(1/2)^(t/13.8)
(7.5/240) = (1/2)^(t/13.8)
0.03125 = (1/2)^(t/13.8)
---
Take the log of both sides to get:
(t/13.8)*log(1/2) = log(0.03125)
---
(t/13.8) = -1.5052/-0.3010
t/13.8 = 5
t = 69 seconds
====================
Cheers,
Stan H.
Answer by ikleyn(53339)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Beryllium-11 decomposes into boron-11 with a half life of 13.8 seconds.
How long will it take 240 g of beryllium-11 to decompose into 7.5 g of berlyium-11?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is very special and very specific.
For the complete solution, there is NO NEED to write many-store complicated exponential functions.
There is a special method and a special approach/reasoning, and this problem
is SPECIALLY CREATED for you to learn this special solution method from me.
Notice that the ratio 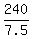 is 32. is 32.
It means that 5 (five) half-lives happened in this decay process
from 240 gram of Beryllium-11 to 7.5 grams of Beryllium-11, because  = 32. = 32.
5 half-lives is 5 times 13.8 seconds, or 5 * 13.8 = 69 seconds.
ANSWER. It will take 69 seconds for 240 grams of Beryllium-11 to decompose into 7.5 grams of Beryllium-11.
*************************************************************
Solved and explained in a way how it SHOULD be done
and how it is EXPECTED to be done.
*************************************************************
|
|
|