Question 239293: When light strikes the surface of a medium such as water or glass, its intensity decreases with depth. The beer-lambert-bougar law states that the percentage of decrease is the same for each additional unit of depth. In a certain lake, intensity decreases about 75% for each additionial meter of depth.
a) Explain why intensity I is an exponential function of depth d in meters
b) Use a formula to express intensity I as an exponential function of d. (use I0 to denote the initial intensity.)
c) Explain in practical terms the meaning of I0.
d) At what depth will the intensity of light be one tenth of the intensity of light striking the surface?
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! Some keys to understanding how to do this problem:- Using percents in formulas or functions is not very practical. So, since 75% is 3/4, we will use 3/4 instead of 75%. (We could also use 0.75 instead of 75%.)
- When problems say "75% of" some number (or "3/4 of") some number, that "of" translates into a multiplication. The beer-lambert-bougar law says that the intensity of light is some percent of the intensity of the light 1 meter above. So to find the intensity of light in your lake, we will multiply the intensity of light above by 75% (or 3/4).
So to figure out the answers to your problem, let's make up a number for the intensity of light just as it hits the water (i.e. the depth is zero):- Let's say the intensity at depth 0 is 100.
- The intensity at a depth of 1 meter would be 3/4 of intensity of the light at 0 meters:
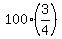 . . - At 2 meters depth the intensity would be 3/4 of the intensity at 1 meters depth:
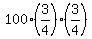 - At 3 meters depth the intensity would be 3/4 of the intensity at 2 meters depth:
 - etc.
a) Explain why intensity I is an exponential function of depth d in meters
We can see that the intensity is calculated, in part, by the repeated multiplication of 3/4. Our formula is an exponential function because we will use an exponent to represent the repeated multiplication of 3/4.
b) Use a formula to express intensity I as an exponential function of d. (use I0 to denote the initial intensity.)
From the example above we can see where the initial intensity (intensity at depth 0) fits in the formula:

where I is the intensity at d meters, 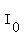 is the initial intensity and d is the depth in meters. is the initial intensity and d is the depth in meters.
c) Explain in practical terms the meaning of 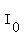 . .
It is the intensity at depth 0 meters
d) At what depth will the intensity of light be one tenth of the intensity of light striking the surface?
One tenth of the intensity of light striking the surface is 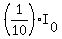 (Remember that "a fraction of a number" means that fraction times that number.) So the equation we need to solve is: (Remember that "a fraction of a number" means that fraction times that number.) So the equation we need to solve is:

First we'll divide by 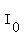

On both sides the 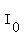 's cancel leaving: 's cancel leaving:

To solve for d, when it is the exponent like this, we will use logarithms:

The left side is -1 because 1/10 is 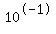 . (If this is not obvious, use your calculator. So now we have: . (If this is not obvious, use your calculator. So now we have:

On the right side we can use the property of logarithms,  , to move the exponent from the argument out in front of the logarithm giving us: , to move the exponent from the argument out in front of the logarithm giving us:

And now we can divide both sides by 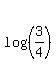 : :

On the right side the 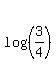 's cancel leaving: 's cancel leaving:

Using our calculator on the remaining log:

And using the calculator to divide we get:

So at very close to 8 meters the intensity of light will be 1/10 of what it was at the surface.
|
|
|