Question 154765: Still don't undertand this and I have a test tomorrow...yikes!!
Here's the question:
A picture that was supposedly painted by Vermeer (1632-1675) contains 99.5% of it's carbon=14. The half life for carbon=14 is 5730 years. Is the picture a fake?
I know the formula to use is(first, Q_0 = Q-naught) Q=Q_0e^-k5730. And I know Q should equal 1/2, but I can't seem to put it all together. Please help!
Thanks,
T
Found 3 solutions by scott8148, jim_thompson5910, stanbon:
Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website! not sure about your formula...
for half-life calculations, you are right - there is a 1/2 in the formula
A=Ao*(1/2)^(t/h)
A is the current amount, Ao is the starting amount, t is the time, h is the half-life
to find the time __ divide by Ao __ A/Ao=.5^(t/h) __ take log __ ln(A/Ao)=(t/h)ln(.5)
divide by ln(.5) __ [ln(A/Ao)]/[ln(.5)]=t/h __ multiply by h __ h{[ln(A/Ao)]/[ln(.5)]}=t
5730[ln(.995)/ln(.5)]=t __ 41.4=t (approx) __ doesn't seem old enough
Answer by jim_thompson5910(35256)  (Show Source):
You can put this solution on YOUR website!  Start with the general exponential formula
Since we're talking about the half life, this means that when  , then  . In other words, when the time is 5,730 years, the amount left over will be half of the original amount.
 Plug in and . This equation represents the half life. We can now solve for the growth/decay constant "k"
 Divide both sides by  .
 Take the natural log of both sides.
 Rewrite the right side using the identity 
 Take the natural log of  to get approximately -0.693147 and take the natural log of "e" to get 1
 Multiply
 Divide both sides by 5,730 to isolate k.
 Divide
So the growth/decay constant is 
So the equation is 
Now I'm assuming that we're using the time frame from 1632 to 1675 (and ignoring the current year 2008). So this would mean that the time span is 1675-1632=43 years. So the claim is that the painting is 43 years old (from the viewpoint of someone living in 1675).
So if the claim is correct, then if  is plugged into the equation , then the resulting amount of carbon should be 99.5% of the original amount. Let's see if this is true:
Start with the given equation.
 Plug in
 Multiply
 Raise "e" to the -0.005203th power to get 0.994811
 Rearrange the terms
If we round to the nearest thousandth, we get
Since 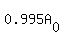 is 99.5% of the original amount , this means that the amount left over is about 99.5% of the original amount. So this shows us that the painting is approximately 43 years old, which means that the painting was most likely created in 1632 (from the viewpoint of 1675). So there is a small chance that this picture is a fake.
Note: we introduced rounding errors due to the evaluation of logarithms and division. So our answer is not accurate.
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website! A picture that was supposedly painted by Vermeer (1632-1675) contains 99.5% of it's carbon=14. The half life for carbon=14 is 5730 years. Is the picture a fake?
I know the formula to use is(first, Q_0 = Q-naught) Q=Q_0e^-k5730. And I know Q should equal 1/2, but I can't seem to put it all together
-----------------------------
Q(t) = Q(o)(1/2)^(t/5730)
0.995Q(0) = Q(o)(1/2)^(t/5730)
0.995 = (1/2)^(t/5730)
ln 0.995 = (t/5730)ln(1/2)
t/5730 = ln 0.995 / ln(1/2)
t/5730 = 0.007232
t = 41.44 years
The picture is a fake.
===================
Cheers,
Stan H.
|
|
|
