Question 1204090: You currently have $6,500 (Present Value) in an account that has an interest rate of 7% per year compounded monthly (12 times per year). You want to withdraw all your money when it reaches $16,250 (Future Value). In how many years will you be able to withdraw all your money? Round your answer to 1 decimal place.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52802)   (Show Source):
You can put this solution on YOUR website! .
If you discard all the verbal husk, then the standard question remains:
How long will it take for the deposit of $6500 to get the value of $16,250,
if the account is compounded monthly at the annual interest of 7% ?
Use the formula for the future value of this compounded account
16250 =  ,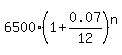
where n is the number of months.
Solve this equation to find n, step by step
 =  ,
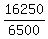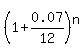2.5 =  .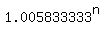
Take logarithm base 10 of both sides
log(2.5) = n*log(1.005833333)
Find n =  = 157.54 months.
Round to the closest  month, in order for the bank was in position
to make the last compounding.
ANSWER. 158 months, or 13 years and 2 months.
Solved.
Notice that in this problem, the answer in decimals is NOT ACCEPTABLE.
The answer must be in months, because the month is THE DISCRETE TIME UNIT
for this problem / (for such problems), due to compounding.
Solving problems for discretely compounded accounts, it is important to understand these things:
(1) The continuous time IS NOT USED and SHOULD NOT be used in the solution,
since the compounding amount IS NOT a continuous function.
The compounded account changes by jumping at the end of each compound period.
(2) The answer must be in integer number of compounding periods;
(3) Your goal is not to get precisely the assigned amount -  .
Your goal is to find the first discrete time, when the compounded account will exceed the assigned amount.
------------------
To see many other similar (and different) solved problems, look into the lesson
- Problems on discretely compound accounts
in this site, and learn the subject from there.
After reading this lesson, you will tackle such problems on your own without asking for help from outside.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Answer: 13.2 years
Work Shown
A = P*(1+r/n)^(n*t)
16250 = 6500*(1+0.07/12)^(12*t)
16250 = 6500*(1.00583333)^(12*t)
16250/6500 = (1.00583333)^(12*t)
2.5 = (1.00583333)^(12*t)
log(2.5) = log( (1.00583333)^(12*t) )
log(2.5) = 12*t*log( 1.00583333 )
t = log(2.5)/( 12*log( 1.00583333 ) )
t = 13.1280168482517
t = 13.2
I rounded up to the nearest tenth.
If we tried t = 13.1, then,
A = P*(1+r/n)^(n*t)
A = 6500*(1+0.07/12)^(12*13.1)
A = 16,218.262943099
A = 16,218.26
We're short of the goal $16,250.
This is why t = 13.1 doesn't work.
But if you tried t = 13.2, then,
A = P*(1+r/n)^(n*t)
A = 6500*(1+0.07/12)^(12*13.2)
A = 16,331.8569055279
A = 16,331.86
We have gone over the goal of $16,250.
|
|
|
