SOLUTION: Hi, I was wondering if I could get some help on this problem? If f(n) = {{{log(n)/log(2006n-n^2)}}}, find f(1) + f(2) + f(3)+...+ f(2005) All I can figure out is the split the lo

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Hi, I was wondering if I could get some help on this problem? If f(n) = {{{log(n)/log(2006n-n^2)}}}, find f(1) + f(2) + f(3)+...+ f(2005) All I can figure out is the split the lo      Log On


   

Question 1203303: Hi, I was wondering if I could get some help on this problem?
If f(n) = 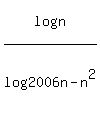log%28n%29%2Flog%282006n-n%5E2%29, find f(1) + f(2) + f(3)+...+ f(2005)
All I can figure out is the split the logarithm on the bottom into 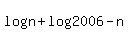log%28n%29+%2B+log%282006+-+n%29
Thank you!
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
If   f(n) = log%28%28n%29%29%2Flog%28%282006n-n%5E2%29%29,    find   f(1) + f(2) + f(3) + . . . + f(2005).
~~~~~~~~~~~~~~~~~~~~~~~~~~~ 


Let m = 2006 - n, and consider the sum of two symmetric terms

    f(n) + f(m) = log%28%28n%29%29%2Flog%28%282006n-n%5E2%29%29 + log%28%28m%29%29%2Flog%28%282006m-m%5E2%29%29.


Notice that  2006m-m^2 = 2006*(2006-n) - (2006-n)^2 = 2006^2 - 2006n - 2006^2 + 2*2006n - n^2 = 2006n-n^2.


So, f(n) and f(m) have THE SAME DENOMINATOR log(2006n-n^2).   


    +---------------------------------------------------------+
    |  This remarkable observation is a KEY to the solution.  |
    +---------------------------------------------------------+


Thus we can write these two addends and their sum with the common denominator

    f(n) + f(m) = log%28%28n%29%29%2Flog%28%282006n-n%5E2%29%29 + log%28%28m%29%29%2Flog%28%282006n-n%5E2%29%29 = %28log%28%28n%29%29+%2B+log%28%28m%29%29%29%2Flog%28%282006n-n%5E2%29%29


which we can continue

    f(n) + f(m) = log%28%28nm%29%29%2Flog%28%282006n-n%5E2%29%29    (1)


Next,  nm = n*(2006-n) = 2006n-n^2,

so, in (1)  the numerator is the same as the denominator.


It gives us  f(n) + f(m) = 1 for each and every pair of positive integers (n,m) such that  m = 2006-n.


Thus the symmetric pairs give the sum of 1 taken 1002 times, i.e. the sum of 1002.


The central (unpaired) term at n= 1003 gives f(n) = f(1003) = log%28%281003%29%29%2Flog%28%282006%2A1003-1003%5E2%29%29 = log%28%281003%29%29%2Flog%28%281003%5E2%29%29 = log%28%281003%29%29%2F%282%2Alog%28%281003%29%29%29 = 1%2F2.


Therefore, the total sum and the  highlight%28highlight%28ANSWER%29%29  is 10021%2F2 = 1002.5.


ANSWER.  The total sum is 10021%2F2 = 1002.5.

Solved.


-----------------


This problem is of a recognized Math Olympiad level.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


This is too nice a problem for us to solve it for you. You should have the pleasure of finding your way to the answer yourself. I will just get you started.

If what I show you doesn't yet help you reach the final answer, then post a "thank you" saying you need more help.

And of course if the little I show you below allows you to finish the problem yourself, I would very much like to see a "thank you" note from you saying so.

By the way, the little you have been able to figure out to do is a BIG first step!

Here is all I am going to show you....

f%281%29=log%281%29%2Flog%281%2A2005%29

f%282005%29+=+log%282005%29%2Flog%282005%2A1%29

Now find the sum of f(1) and f(2005) and use basic rules of logarithms to simplify....

Then a little logical reasoning and simple mental arithmetic should lead you to the final answer.

Best of luck. I hope to hear from you one way or another...!

Note: After you finish the problem, I will post a full answer so other students in the future can see it.

---------------------------------------------------------------

Thanks for the note of thanks.

It looks as if you were able to finish the problem on your own using my suggestion, even though two other tutors posted full solutions....

Good job!

Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Claim:
f(n) + f(2006-n) = 1 where n is an integer in the set {1,2,3,...,2005}

Here's a proof:
f%28n%29+=+log%28%28n%29%29%2Flog%28%282006n-n%5E2%29%29

f%28n%29+=+log%28%28n%29%29%2Flog%28%28n%282006-n%29%29%29

f%282006-n%29+=+log%28%282006-n%29%29%2Flog%28%28%282006-n%29%282006-%282006-n%29%29%29%29

f%282006-n%29+=+log%28%282006-n%29%29%2Flog%28%28%282006-n%29%282006-2006%2Bn%29%29%29

f%282006-n%29+=+log%28%282006-n%29%29%2Flog%28%28%282006-n%29n%29%29

f%282006-n%29+=+log%28%282006-n%29%29%2Flog%28%28n%282006-n%29%29%29
Both f(n) and f(2006-n) have the same denominator.

It allows us to add the numerators and use the log rule log(A)+log(B) = log(AB)




f%28n%29%2Bf%282006-n%29+=+%28log%28%28n%282006-n%29%29%29%29%2Flog%28%28n%282006-n%29%29%29

f%28n%29%2Bf%282006-n%29+=+1

Then using that formula we can write
f(1) + f(2005) = 1
f(2) + f(2004) = 1
f(3) + f(2003) = 1
f(4) + f(2002) = 1
...
...
f(2002) + f(4) = 1
f(2003) + f(3) = 1
f(2004) + f(2) = 1
f(2005) + f(1) = 1
We have 2005 pairs of values. Each pair adds to 1.
We have a sum of 1+1+1+...+1 = 2005*1 = 2005

This appears it could be the final answer. However, it is not. Pay close attention that double-counting has taken place here.
For instance, f(1)+f(2005) would be treated the same as f(2005)+f(1).

To correct this error, divide by 2.
2005/2 = 1002.5

Put another way, if we add straight down through all 2005 equations and do a bit of algebraic housekeeping, the left hand sides combine to:
2*( f(1)+f(2)+f(3)+...+f(2005) )
while the right hand sides combine to 1+1+1+..+1, aka 2005 copies of '1' being added.
Therefore, we have the equation
2*( f(1)+f(2)+f(3)+...+f(2005) ) = 2005
which rearranges to
f(1)+f(2)+f(3)+...+f(2005) = 2005/2 = 1002.5



Answer:
f(1) + f(2) + f(3)+...+ f(2005) = 1002.5