SOLUTION: Aplique a propriedade do logaritmo Log2 (4x2)

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Aplique a propriedade do logaritmo Log2 (4x2)      Log On


   

Question 1198695: Aplique a propriedade do logaritmo
Log2 (4x2)
Found 4 solutions by MathLover1, Alan3354, math_tutor2020, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
log%282%2C4x%5E2%29++=+log%282%2C4%29+%2B+log%282%2Cx%5E2%29
= 2+%2B+log%282%2Cx%5E2%29
---
Or, 2+%2B+2log%282%2Cx%29
---
Or, 2%2A%281+%2B+log%282%2Cx%29%29

Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Method 1
log%282%2C%284x%5E2%29%29+=+log%282%2C%284%29%29%2Blog%282%2C%28x%5E2%29%29 Use log rule log(A*B) = log(A)+log(B)

log%282%2C%284x%5E2%29%29+=+log%282%2C%282%5E2%29%29%2Blog%282%2C%28x%5E2%29%29

log%282%2C%284x%5E2%29%29+=+2%2Alog%282%2C%282%29%29%2B2%2Alog%282%2C%28x%29%29 use rule log(A^B) = B*log(A)

log%282%2C%284x%5E2%29%29+=+2%2A1%2B2%2Alog%282%2C%28x%29%29

log%282%2C%284x%5E2%29%29+=+2%2B2%2Alog%282%2C%28x%29%29

log%282%2C%284x%5E2%29%29+=+2%281%2Blog%282%2C%28x%29%29%29

---------------------------------------------------
Method 2

log%282%2C%284x%5E2%29%29+=+log%282%2C%28%282x%29%5E2%29%29

log%282%2C%284x%5E2%29%29+=+2%2Alog%282%2C%282x%29%29 Use rule log(A^B) = B*log(A)

log%282%2C%284x%5E2%29%29+=+2%2A%28log%282%2C%282%29%29%2Blog%282%2C%28x%29%29%29 Use log rule log(A*B) = log(A)+log(B)

log%282%2C%284x%5E2%29%29+=+2%2A%281%2Blog%282%2C%28x%29%29%29

log%282%2C%284x%5E2%29%29+=+2%2B2%2Alog%282%2C%28x%29%29

I'll leave it up to you whether you want it factored or not.

You can use a graphing tool like Desmos or GeoGebra to visually confirm the answer.

Keep in mind that the domain of the right-hand-side is +x+%3E+0+ so that the output is a real number.
If x+%3C+0, then the right-hand-side result is some complex number in the form a%2Bbi such that i+=+sqrt%28-1%29

Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
Aplique a propriedade do logaritmo
Log2 (4x2)
~~~~~~~~~~~~~~~~~


        This problem, harmless at first sight,  has a huge underwater stone,  like a trap,
        which was overlooked by other tutors. 


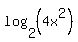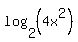We start from this expression  log%282%2C%284x%5E2%29%29.


In this expression, x can be any non-zero number, negative or positive.


In other words, the domain, where the expression is defined / (makes sense), 
is the set of all real non-zero numbers {R \ {0} }.


In this domain

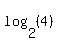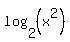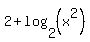    log%282%2C%284x%5E2%29%29 = log%282%2C%284%29%29 + log%282%2C%28x%5E2%29%29 = 2+%2B+log%282%2C%28x%5E2%29%29.



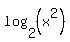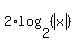Now,  log%282%2C+%28x%5E2%29%29 = 2%2Alog%282%2C%28abs%28x%29%29%29  is valid for all values of x in the domain, positive or negative,
excluding the zero value of x.  Notice the absolute value sign under the logarithm.


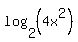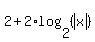Therefore, in the entire domain,  log%282%2C%284x%5E2%29%29 = 2+%2B+2%2Alog%282%2C%28abs%28x%29%29%29.


It does not matter if you take the factor of "2" outside the parentheses or not.


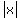What is REALLY IMPORTANT, is to use the sign of absolute value,  abs%28x%29,  under the logarithm 
in the final expression.


Then (and only then) the identity 

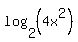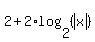    log%282%2C%284x%5E2%29%29 = 2+%2B+2%2Alog%282%2C%28abs%28x%29%29%29.


is valid on the entire domain, which is  {R \ {0} }, the set of all real non-zero numbers.

Solved.

---------------

The meaning of this assignment is to simplify the given expression accurately over the entire domain.