Question 1192399: Not sure what to do.
The following table represents the number of koala bears alive since the year 2000. Write a function for the koala bear population, P(t), as a function of t, the time in years since 2000.
1(time since 2000)-------------------P(population of koala bears)
0 --------------------------- 100,000
1---------------------------- 93,500
2---------------------------- 87,423
21--------------------------- 24,381
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Not sure what to do.
The following table represents the number of koala bears alive since the year 2000.
Write a function for the koala bear population, P(t), as a function of t, the time in years since 2000.
1(time since 2000)-------------------P(population of koala bears)
0 --------------------------- 100,000
1---------------------------- 93,500
2---------------------------- 87,423
21--------------------------- 24,381
~~~~~~~~~~~~~~~~~~~
Looking into the table, we see that the number of koala bears k(x) is decreasing with years.
It is naturally to assume that we have decaying exponential function.
To check it, calculate the ratios for consecutive years
 = =  = 0.935, = 0.935, 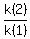 = = 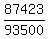 = 0.935.
Thus we see that we have a geometric progression with the common ratio r = 0.935.
To check it, calculate k(21) using the formula for geometric progression
k(21) = = 0.935.
Thus we see that we have a geometric progression with the common ratio r = 0.935.
To check it, calculate k(21) using the formula for geometric progression
k(21) = 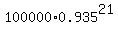 = 24381.
Comparing it with the last value in the Table, you see that you have every reason to use the formula
of geometric progression
k(x) = = 24381.
Comparing it with the last value in the Table, you see that you have every reason to use the formula
of geometric progression
k(x) = 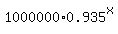 (1)
to calculate the population of koal bears k(x) in the entire interval 0 <= x <= 21,
where x denotes the years since 2000. (1)
to calculate the population of koal bears k(x) in the entire interval 0 <= x <= 21,
where x denotes the years since 2000.
Exponential functions of the type (1) are typical functions to predict population growth/decay.
---------------
Solved and explained.
If you want to see many other similar and different solved problems on population growth, look into the lesson
- Population growth problems
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|