Question 1187575: A radioactive form of uranium has a half life of 2.5x 10^5 years. a) Find the remaining mass of 1 g sample after t years
b) Determine the remaining mass of this sample after 5000 years.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the radioactive form of uranium has a half life of 2.5 * 10^5 years.
the formula is f = p * e^(rt).
r is the rate of growth per year.
t is the time in years.
if the future value of the uranium is equal to half the present value of the uranium, then the formula becomes:
1/2 = e^(rt)
if the time to half life is equal to 2.5 * 10^5 years, then the formula becomes:
1/2 = e^(r * 2.5 * 10^5)
take the natural log of both sides of the equation to get:
ln(1/2) = ln(e ^ (r * 2.5 * 10^5))
since ln(e ^ (r * 2.5 * 10^5)) is equal to r * 2.5 * 10^5 * ln(e) and since ln(e) = 1, the formula becomes:
ln(1/2) = r * 2.5 * 10^5
divide both sides of the equation by (2.5 * 10^5) to get:
ln(1/2) / (2.5 * 10^5) = r
solve for r to get:
r = -2.77258872 * 10^-6
to see if that value is good, replace r in the original equation with that and find f.
the original equation is f = p * e^(rt)
when p = 1, the equation becomes:
f = e^(rt)
when r = -2.77258872 * 10^-6 and t = 2.5 * 10^5, the formula becomes:
f = e ^ (-2.77258872 * 10^-6 * 2.5 * 10^5)
solve for f to get:
f = .5.
the formula is good and the rate of growth is -2.77258872 * 10^-6 per year.
the remaining mass of 1 gram of uranium after t years is given by the formula:
f = 1 * e ^ ((-2.77258872 * 10^-6 * t)
when t = 5000, the formula becomes:
f = 1 * e ^ ((-2.77258872 * 10^-6 * 5000)
solve for f to get:
f = .9862327045 grams.
you can graph the equation.
here's what it looks like.
it shows the values of f (represented by y in the graph) for t (represented by x in the graph) at 5000 years and at 2.5 * 10^5 years in the future.

Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A radioactive form of uranium has a half life of 2.5x 10^5 years.
a) Find the remaining mass of 1 g sample after t years
b) Determine the remaining mass of this sample after 5000 years.
~~~~~~~~~~~~~~
In his post, @Theo makes tons of absolutely unnecessary work, unnecessary calculations
and unnecessary explanations, making simple problem hopelessly confused and showing you WRONG WAY doing job.
Had some student come to his teacher and present a solution like @Theo does in his post,
the teacher would only shrug shoulders (out of curtesy).
I came with two goals: 1) to make the solution in a regular/normal simple manner, and
2) to make the solution in a way HOW TO it should be done and presented.
Since the half life is given, we write the decay equation using the " base 2 " exponent function
m(t) =  for a current mass m(t), where m(0) is the initial mass of the sample.
Now we simply substitute the given values into the formula and calculate
(a) 1 gram sample after t years m(t) =
for a current mass m(t), where m(0) is the initial mass of the sample.
Now we simply substitute the given values into the formula and calculate
(a) 1 gram sample after t years m(t) = 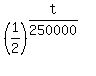 grams.
(b) the remaining mass of this sample after 5000 years is m(5000) = grams.
(b) the remaining mass of this sample after 5000 years is m(5000) = 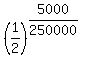 = = 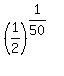 = = 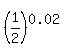 = 0.9862327. ANSWER = 0.9862327. ANSWER
That is all. The problem is just solved and completed.
What you need to know to solve such problems, is THIS:
- there are different forms of exponential decay equations: 1) ekt-form; 2) " base 2 " form; and 3) an arbitrary " base b " form.
- each form is good for its own purposes and problems;
- if the problem's data is given in half-life terms, always use " base 2 " form and make all calculations in this form;
do not change this form in the course of the solution, until the problem asks you to change the base explicitly.
//////////////
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|