Question 1169252: The count in a bateria culture was 400 after 10 minutes and 1200 after 30 minutes. Assuming the count grows exponentially,
What was the initial size of the culture?
Find the doubling period.
Find the population after 80 minutes.
When will the population reach 14000.
Found 2 solutions by Boreal, Theo:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! A=Aob^x
400=Ao^b^10
1200=Ao^b^30
3=b^20
b=3^(1/20)=1.056
not rounding
1200=Aob^30=Ao*3^1.5
Ao=230.94 or 231 organisms
-
A=231*3^0.05^x
Doubling is when
2=3^0.05^x
or ln 2=x ln 3^0.05
ln2=0.05x ln 3
20 ln2=x ln3
x=12.619 min or 12.6 min.
-
tripling time is 3=1.056^x or
20 ln 3=x ln 3
x=20 minutes, which it should be.
-
after 80 minutes
A=231(3^0.05)^80=231^3^4
=18,711 organisms
-
14000=231*3^0.05x
60.606=3^(0.05)^x
ln 60.606=x*0.05 ln 3
82.088=x ln3
x=74.72 min
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! culture grows to 400 after 10 minutes and to 1200 after 30 minutes.
growth is exponential.
exponential formula is y = a * b^x
x would be the number of minutes.
the count in bacteria went from 400 to 1200 in 20 minutes.
set y = 1200 and a = 400 to get:
1200 = 400 * b^20
divide both sides of the equation by 200 to get:
1200/400 = b^20
simplify to get:
3 = b^20
take the 20th root of both sides of the equation to get:
3^(1/20) = b
solve for b to get:
b = 3^(1/20) = 1.056467309
b should be the growth factor per minute.
if you start with 400 and grow it exponentially for 20 minutes, then you get:
400 * 1.056467309^20 = 1200.
this confirms the growth factor per minute is good.
if it's 400 after 10 minutes and you want to find out what it was in the beginning, then divide by the growth factor raised to 10 minutes to get:
400 / 1.056467309^10 = 230.9401077.
to find out when it will grow to 14000 from when it was started, take 230.9401077 and multiply it by 1.056467309 raised to the nth power to get:
1400 = 230.9401077 * 1.056467309^n
divide both sides of this equation by 230.9401077 to get:
1400/230.9401077 = 1.056467309^n
take the log of both sides of this equation to get:
log(14000/230.9401077) = log(1.056467309^n)
this becomes:
log(14000/230.9401077) = n*log(1.056467309)
divide both sides of this equation by log(1.056467309) to get:
log(14000/230.9401077)/log(1.056467309) = n
solve for n to get:
n = 74.7243454 minutes.
to confirm:
replace n in the original equation by its calculated value to get:
y = 230.9401077 * 1.056467309^74.7243454
solve for y to get:
y = 14000
this confirms the solution is correct.
the questions to be answered are:
Find the doubling period.
the doubling period can be found as follows:
let y = 2 and a = 1.
the formula becomes 2 = 1 * 1.056467309^n
simplify to get:
2 = 1.056467309^n
take the log of both sides of the equation to get:
log(2) = log(1.056467309^n)
this becomes log(2) = n * log(1.056467309)
divide both sides of the equation by log(1.056467309) to get:
log(2)/log(1.056467309) = n
solve for n to get:
n = 12.61859507
conform by taking y = 1.056467309^12.61859507 to get:
y = 2.
this confirms the doubling formula is good.
the doubling period is 12.61859507 minutes.
Find the population after 80 minutes.
the population in 80 minutes from the initial size of the culture would be:
y = 230.9401077 * 1.056467309^80 = 18706.14872.
When will the population reach 14000.
the population from the initial size of the culture to 14000 would happen in 74.7243454 minutes.
this was already solved above.
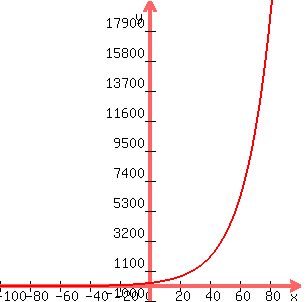
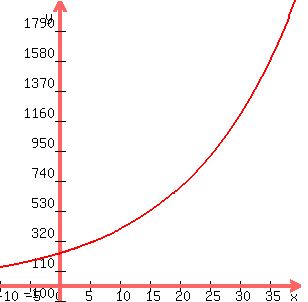
i graphed the equation.
the results are shown below:

the shows the following:
at 0 minutes, the bacteria count was 230.94.
at 10 minutes the bacteria count was 400.
at 1200 minutes, the bacteria count was 1200.
at 42.619 minutes (12.619 minutes after 30 minutes), the count was 2400.
12.619 minutes was the doubling period.
at 74.724 minutes, the count was 14000.
at 80 minutes, the count was 18706.149.
all these number confirm the equation is correct.
the equation is y = a*b^x which becomes:
y = 230.9401077 * 1.056467309^x, where x is the number of minutes from the start of the culture.
|
|
|