|
Question 207968: I have four problems to use this with if you could help me with one it would be great thanks.An operation $ has been defined over the set of natural numbers. in each case, find 2$3, determine whether or not the set of natural numbers is closed under $, determine if $ is commutative and determine if is associative.
x$y=(1+x)+y
Found 2 solutions by jim_thompson5910, stanbon:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! Since the general expression is x$y, to find 2$3, simply plug in x=2 and y=3 into 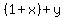 and evaluate the expression. I'll let you do that.
To find out if the operation is closed, you need to ask yourself: if I plug in two arbitrary natural numbers, will I always get a natural number out? The answer is yes. Why? Recall that the sum of two natural numbers is a natural number. Since 1 is a natural number, 1+x is also a natural number. Finally, (1+x)+y is a natural number (given that x and y are natural numbers). So this shows us that $ is closed under the set of natural numbers.
As for commutativity, we need to determine if x$y=y$x. In terms of the definition, this means that we need to see if  (just switch each instance of x and y) is an identity. I'll let you determine that.
To determine associativity, you need to determine if (x$y)$z=x$(y$z). If you can show that (by using the definition), then you can show that $ is associative.
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website! An operation $ has been defined over the set of natural numbers. in each case, find 2$3, determine whether or not the set of natural numbers is closed under $, determine if $ is commutative and determine if is associative.
----------------------------
x$y=(1+x)+y
Then 2$3 = (1+2)+3 = 6
------------------------------------
Naturals closed under $ ?
Let a and b be natural numbers
Then a$b = (1+a)+b = 1+(a+b)
Since the natural numbers are closed under addition,
1 + (a+b) is is a natural number. So the set of
natural numbers is closed under $.
------------------------------------
Is # communtative?
Show that a$b = b$a
(1+a)+b = (1+b)+a
1 + a + b = 1+ b + a
Since the naturals are commutative,
1 + a + b = 1 + a+b
--------------------------
Is $ associative?
Show that (a$b)$c = a$(b$c)
============
Can you do that?
Cheers,
Stan H.
|
|
|
| |
