|
Question 1209235: Find the number of ordered pairs (m,n) of integers that satisfy
mn = 3m + 3n + 17.
Found 4 solutions by greenestamps, AnlytcPhil, ikleyn, math_tutor2020:
Answer by greenestamps(13295)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Solve the equation for one variable in terms of the other:



Perform the indicated division and express the result as quotient and remainder:


In that last equation, m and 3 are integers, so 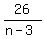 must be an integer. must be an integer.
The number of ordered pair solutions is the number of integer factors of 26, which is 4.
NOTE: In typical problems like this, we are looking for solutions in positive integers. However, this problem does not specify positive integers; counting positive and negative integers, the number of integer factors of 26 is 8.
So there are 8 ordered pair solutions.
ANSWER: 8
The problem doesn't ask us to find the solutions, but we can do so to verify that there are 4 pairs of solutions. Note that the expression is symmetrical in m and n, so if (a,b) is a solution the (b,a) will be a solution. So to find the 8 solutions we only need to find 4 of them and switch the order of the two numbers to get the other solutions.
n-3 n m=3+26/(n-3) solutions (m,n)
---------------------------------------
1 4 3+26/1 = 29 (4,29) and (29,4)
2 5 3+26/2 = 16 (5,16) and (16,5)
-1 2 3+26/-1 = -23 (2,-23) and (-23,2)
-2 1 3+26/-2 = -10 (1,-10) and (-10,1)
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!



 Long division:
3
n-3)3n+17
3n- 9
26
Long division:
3
n-3)3n+17
3n- 9
26
  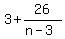 n-3 must divide evenly into 26, so n-3 is either ±1,±2,±13, or ±26
That's 8 possibilities, so we know the answer is 8. To check, we find them:
1. if n-3 = -26, then n = -23, and m = 3+26/(-23-3) = 2, ordered pair (2,-23).
2. if n-3 = -13, then n = -10, and m = 3+26/(-10-3) = 1, ordered pair (1,-10).
3. if n-3 = -2, then n = 1, and m = 3+26/(1-3) = -10, ordered pair (-10,1).
4. if n-3 = -1, then n = 2, and m = 3+26/(2-3) = -23, ordered pair (-23,2).
5. if n-3 = 1, then n = 4, and m = 3+26/(4-3) = 29, ordered pair (29,4).
6. if n-3 = 2, then n = 5, and m = 3+26/(5-3) = 16, ordered pair (16,5).
7. if n-3 = 13, then n = 16, and m = 3+26/(16-3) = 5, ordered pair (5,16).
8. if n-3 = 26, then n = 29, and m = 3+26/(29-3) = 4, ordered pair (4,29).
So indeed, there are 8 such ordered pairs.
Here is a plot of all 8. See how nicely they fit on that curve.
Can you guess what the equation of that curve is?
n-3 must divide evenly into 26, so n-3 is either ±1,±2,±13, or ±26
That's 8 possibilities, so we know the answer is 8. To check, we find them:
1. if n-3 = -26, then n = -23, and m = 3+26/(-23-3) = 2, ordered pair (2,-23).
2. if n-3 = -13, then n = -10, and m = 3+26/(-10-3) = 1, ordered pair (1,-10).
3. if n-3 = -2, then n = 1, and m = 3+26/(1-3) = -10, ordered pair (-10,1).
4. if n-3 = -1, then n = 2, and m = 3+26/(2-3) = -23, ordered pair (-23,2).
5. if n-3 = 1, then n = 4, and m = 3+26/(4-3) = 29, ordered pair (29,4).
6. if n-3 = 2, then n = 5, and m = 3+26/(5-3) = 16, ordered pair (16,5).
7. if n-3 = 13, then n = 16, and m = 3+26/(16-3) = 5, ordered pair (5,16).
8. if n-3 = 26, then n = 29, and m = 3+26/(29-3) = 4, ordered pair (4,29).
So indeed, there are 8 such ordered pairs.
Here is a plot of all 8. See how nicely they fit on that curve.
Can you guess what the equation of that curve is?
 Edwin
Edwin
Answer by ikleyn(53614)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of ordered pairs (m,n) of integers that satisfy
mn = 3m + 3n + 17.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Transform the given equation this way
mn - 3m - 3n + 9 = 26,
(n-3)*(m-3) = 26.
So, n-3 and m-3 are divisors of 26.
There are 4 different decompositions of 26 into the product of positive integer numbers
8 = 1*26 = 2*13 = 13*2 = 26*1
It gives 4 different pairs (m,n). // Since the problem does not ask to find them,
I will not find them.
There are 4 different decompositions of 26 into the product of negative integer numbers
26 = (-1)*(-26) = (-2)*(-13) = (-13)*(-2) = (-26)*(-1).
It gives 4 other different pairs (m,n). // Since the problem does not ask to find them,
I will not find them.
In all, there are 4+4 = 8 different pairs of integer numbers, satisfying the given equation.
Solved.
Answer by math_tutor2020(3832)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 8
Work Shown
mn = 3m+3n+17
mn-3m-3n = 17
mn-3m-3n+9 = 17+9
(mn-3m)+(-3n+9) = 26
m(n-3)-3(n-3) = 26
(m-3)(n-3) = 26
n = 26 = 2^1*13^1 = p^a*q^b shows that a = 1, b = 1
d(n) = number of positive divisors of n
n = p^a*q^b
d(n) = (1+a)*(1+b)
d(26) = (1+1)*(1+1)
d(26) = 4
There are 4 positive divisors of 26 and they are: 1, 2, 13, 26.
When including the negative divisors we get 8 total divisors:
1, 2, 13, 26,
-1, -2, -13, -26
So there must be 8 ordered pairs (m,n) that make (m-3)(n-3) = 26 true and that make m*n = 3m+3n+17 true as well; where m,n are integers.
If m,n were allowed to be decimal numbers, then there would be infinitely many ordered pair solutions.
-----------------------
Extra info:
If you want to find each ordered pair, then set the factors m-3 and n-3 equal to the factors of 26.
Some examples:
m-3 = 1 and n-3 = 26 lead to (m,n) = (4,29)
m-3 = 2 and n-3 = 13 lead to (m,n) = (5,16)
m-3 = 13 and n-3 = 2 lead to (m,n) = (16,5)
Here are all 8 integer solutions
(-23,2), (-10,1), (1,-10), (2,-23),
(4,29), (5,16), (16,5), (29,4)
They are sorted from smallest x coordinate to the largest x coordinate.
We have symmetry going on since (5,16) swaps to (16,5) as one example.
Side notes: - x*y = 3x+3y+17 solves to y = (3x+17)/(x-3)
- If you graphed y = (3x+17)/(x-3) using a tool like Desmos or GeoGebra (among many others), you can then determine the locations of the lattice points. A lattice point (x,y) is where both x and y are integers.
|
|
|
| |