Special advanced problems on finding the range of functions
Problem 1
Find the domain, the range and intercepts of the function f(x) = x^2 + x - 1.
Solution
(1) The domain of this function is the set of all real numbers.
In other words, the domain is the entire number line, from  to
to  .
Question (1) is complete.
(2) This function represents a parabola,
Since the coefficient at x^1 is positive (it is 1 (one)), the parabola has the minimum.
The range of this function is the set of its values, and it is the set of all real numbers
from the minimum of the parabola to infinity.
So, to determine the range, we need to determine the minimum.
The minimum of any quadratic function y = ax^2 + bx + c with positive coefficient "a" is at
.
Question (1) is complete.
(2) This function represents a parabola,
Since the coefficient at x^1 is positive (it is 1 (one)), the parabola has the minimum.
The range of this function is the set of its values, and it is the set of all real numbers
from the minimum of the parabola to infinity.
So, to determine the range, we need to determine the minimum.
The minimum of any quadratic function y = ax^2 + bx + c with positive coefficient "a" is at
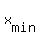 =
=  .
In our case it is
.
In our case it is 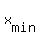 =
= 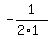 =
=  = -0.5.
The minimum is
= -0.5.
The minimum is  =
= 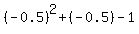 = 0.25 - 0.5 - 1 = -1.25.
Therefore, the range of this quadratic function is from -1.25 to infinity.
In the interval form, the range is [-1.25,
= 0.25 - 0.5 - 1 = -1.25.
Therefore, the range of this quadratic function is from -1.25 to infinity.
In the interval form, the range is [-1.25, ).
Thus question (2) is complete.
(3) To find x-intercepts, you need to solve this equation
x^2 + x - 1 = 0.
Use the quadratic formula
).
Thus question (2) is complete.
(3) To find x-intercepts, you need to solve this equation
x^2 + x - 1 = 0.
Use the quadratic formula
 =
= 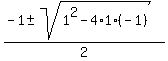 =
= 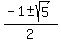 .
The roots are
.
The roots are  =
= 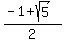 = 0.618033989 (approximate),
and
= 0.618033989 (approximate),
and  =
= 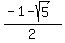 = -1.618033989 (approximate).
= -1.618033989 (approximate).
Problem 2
Find the range of the function f(x) = 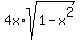 algebraically
algebraically
Solution
Let real number "t" belongs to the range. It means that
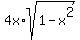 = t (1)
for some value of x. Square bot sides of (1). You will get
= t (1)
for some value of x. Square bot sides of (1). You will get
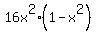 = t^2
= t^2
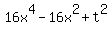 = 0. (2)
You can consider equation (2) as a quadratic equation relative
= 0. (2)
You can consider equation (2) as a quadratic equation relative  .
The condition that it has a real solution for
.
The condition that it has a real solution for  is this inequality for the discriminant
is this inequality for the discriminant
 >= 0, or
>= 0, or 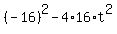 >= 0, or 256 >=
>= 0, or 256 >= 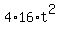 .
It implies
.
It implies  <= 4; hence, |t| <= 2, or -2 <= t <= 2.
Thus, equation (1) has a real solution if and only if -2 <= t <= 2.
So, the range of the function
<= 4; hence, |t| <= 2, or -2 <= t <= 2.
Thus, equation (1) has a real solution if and only if -2 <= t <= 2.
So, the range of the function 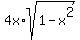 is this interval -2 <= t <= 2, or t belongs [-2,2]. ANSWER
is this interval -2 <= t <= 2, or t belongs [-2,2]. ANSWER
Surely, this problem can be solved using Calculus, but it will require painstaking calculations.
Alternatively, this problem can be solved in this simple way using elementary Algebra much easier than applying Calculus.
Surely, the Calculus approach is like a heavy army tank: it is universal and works everywhere.
So, if you know Calculus and do not afraid to apply it, boldly go forward.
But if the teacher gave you similar problem long before you learn Calculus,
know and remember that this elementary Algebra method probably works.
Problem 3
Find the range of the function f(x) = 2x + 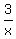 algebraically.
algebraically.
Solution
They ask about the range of this function f(x) = 2x + 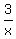 .
The plot is shown under this link
https://www.desmos.com/calculator/lh7qjcdhic
https://www.desmos.com/calculator/lh7qjcdhic
The range is the set of real values t such that
2x +
.
The plot is shown under this link
https://www.desmos.com/calculator/lh7qjcdhic
https://www.desmos.com/calculator/lh7qjcdhic
The range is the set of real values t such that
2x + 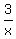 = t for some x.
In other words, the range is the set of real numbers t such that the quadratic equation
2x^2 + 3 = tx, or 2x^2 - tx + 3 = 0
has real solutions for x.
For it, the necessary and sufficient condition is that the discriminant is non-negative
d = (-t)^2 - 4*2*3 >= 0, or t^2 >= 24, or |t| >=
= t for some x.
In other words, the range is the set of real numbers t such that the quadratic equation
2x^2 + 3 = tx, or 2x^2 - tx + 3 = 0
has real solutions for x.
For it, the necessary and sufficient condition is that the discriminant is non-negative
d = (-t)^2 - 4*2*3 >= 0, or t^2 >= 24, or |t| >=  , or
+------------------------------------+
| t <=
, or
+------------------------------------+
| t <= 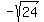 or t >=
or t >=  . |
+------------------------------------+
Thus the range of the function (fxg) is the union of the two sets
(
. |
+------------------------------------+
Thus the range of the function (fxg) is the union of the two sets
( ,
,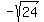 ] U [
] U [ ,
, ). ANSWER
). ANSWER
Problem 4
Find the range of function f(x) = 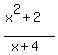 algebraically.
algebraically.
Solution
Let real number "t" belongs to the range. It means that
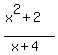 = t (1)
for some value of x. Step by step, reduce equation (1) to standard form quadratic equation
= t (1)
for some value of x. Step by step, reduce equation (1) to standard form quadratic equation
 =
=  ,
,
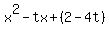 = 0. (2)
Equation (2) is a standard form quadratic equation
= 0. (2)
Equation (2) is a standard form quadratic equation  = 0 with coefficients
a = 1, b = -t, c = 2-4t.
The condition that it has a real solution for
= 0 with coefficients
a = 1, b = -t, c = 2-4t.
The condition that it has a real solution for  is this inequality for the discriminant
is this inequality for the discriminant
 >= 0, or
>= 0, or 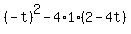 >= 0, or t^2 + 16t -8 >= 0.
The roots of this quadratic equation for t are
>= 0, or t^2 + 16t -8 >= 0.
The roots of this quadratic equation for t are
 =
=  =
= 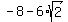 = -16.4853 (rounded) and
= -16.4853 (rounded) and  =
= 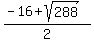 =
=  = 0.4853 (rounded).
The discriminant is non-negative if and only if value of "t" is out of the roots' interval
t <=
= 0.4853 (rounded).
The discriminant is non-negative if and only if value of "t" is out of the roots' interval
t <= 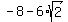 = -16.4853 or t >=
= -16.4853 or t >=  =0.48528.
Therefore, equation (1) has a real solution if and only if
=0.48528.
Therefore, equation (1) has a real solution if and only if  < t <=
< t <= 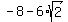 or
or  <= t <
<= t <  .
Thus the range of the function f(x) = (x^2 + 2)/(x + 4) is the union of these intervals (
.
Thus the range of the function f(x) = (x^2 + 2)/(x + 4) is the union of these intervals ( ,
,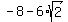 ] and [
] and [ ,
, ).
ANSWER. The range of the function
).
ANSWER. The range of the function 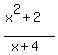 is the union of these intervals (
is the union of these intervals ( ,
,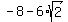 ] and [
] and [ ,
, ).
).
It is how to solve this problem using only elementary Algebra and without using Calculus.
Problem 5
The domain of the function r(x) = 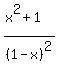 is (-oo,1) U (1,oo). What is the range?
is (-oo,1) U (1,oo). What is the range?
Solution
Real number "t" belongs to the range of this function if and only if
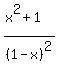 = t for some real x. (1)
Rewrite (1) in an equivalent form
= t for some real x. (1)
Rewrite (1) in an equivalent form
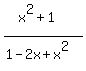 = t,
= t,
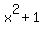 =
= 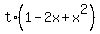 ,
x^2 + 1 = tx^2 - 2tx + t,
(1-t)x^2 + 2tx + (1-t) = 0.
This last quadratic equation has a real solution IF and ONLY IF the discriminant is non-negative
d = b^2 - 4ac >= 0,
or
(2t)^2 - 4*(1-t)*(1-t) >= 0,
4t^2 - 4*(1-t)^2 >= 0,
t^2 - 1 + 2t - t^2 >=0,
2t >= 1,
t >= 1/2.
At this point, the solution is complete.
ANSWER. The domain is the set of all real numbers greater than or equal to 1/2.
,
x^2 + 1 = tx^2 - 2tx + t,
(1-t)x^2 + 2tx + (1-t) = 0.
This last quadratic equation has a real solution IF and ONLY IF the discriminant is non-negative
d = b^2 - 4ac >= 0,
or
(2t)^2 - 4*(1-t)*(1-t) >= 0,
4t^2 - 4*(1-t)^2 >= 0,
t^2 - 1 + 2t - t^2 >=0,
2t >= 1,
t >= 1/2.
At this point, the solution is complete.
ANSWER. The domain is the set of all real numbers greater than or equal to 1/2.
It is how to solve this problem using only elementary Algebra and without using Calculus.
My other lessons in this site on plotting and analyzing functions are
- Finding x-intercepts and y-intercepts
- Compressing and stretching graphs
- HOW TO PLOT transformed functions
- HOW TO write functions for transformed plots
- HOW TO PLOT transformed periodic trigonometry functions
- Analyzing periodic trigonometric functions for the amplitude, the period, vertical and horizontal shifts
- Do not fall into a TRAP when analyzing problems on trigonometric functions
- The domain and the range of transformed functions
- Write a function which is a result of given transformations of the parent function
- Describe transformations from the given parent function to final function
- Writing a function rule for a function based on its wording description
- Constructing a function based on its given properties
- Finding inverse functions
- Miscellaneous problems on plots of functions
- Given a point on a plot of a function, find the corresponding point on the plot of transformed function
- Special advanced problems on finding the domain of functions
- OVERVIEW of lessons on plotting and analyzing functions
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

