SOLUTION: The points(-1,-7) and (5,10) are the endpoints of the diameter of a circle. Graph the circle. Find an equation of the circle. Cordinates of Midpoint of diameter of a circle=((x

Algebra ->  Coordinate-system -> SOLUTION: The points(-1,-7) and (5,10) are the endpoints of the diameter of a circle. Graph the circle. Find an equation of the circle. Cordinates of Midpoint of diameter of a circle=((x      Log On


   

Question 262337: The points(-1,-7) and (5,10) are the endpoints of the diameter of a circle. Graph the circle. Find an equation of the circle. Cordinates of Midpoint of diameter of a circle=((x1 x2)/2, (y1 y2)/2): ((-1 5)/2, (-7 10)/2)=(2, 3/2). Where a=2 and b=3/2, radius r^2 =(a-x1)^2 (b-x2)^2: r^2=(2--1)^2 (3/2--7)^2, r=9.01. Eqn of circle: (x-a)^2 (y-b)^2=r^2: (x-2)^2 (y-3/2)^2=81.25.
Found 3 solutions by solver91311, Theo, cov20:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


If you know the endpoints of the diameter of a circle, you can use the midpoint formulas to calculate the midpoint of the diameter which is the center of the circle. Then the distance formula can be used to calculate the distance from the center to either endpoint of the diameter which is equal to the radius of the circle.

The -coordinate of the mid-point of the diameter segment, and therefore the -coordinate of the center of the circle is given by:



and the -coordinate of the mid-point of the diameter segment, and therefore the -coordinate of the center of the circle is given by:



Where and are the coordinates of the endpoints of the diameter.

The measure of the segment from the center of the circle, , to either endpoint of the diameter, either or is given by the distance formula:



(or if you prefer)

To graph, set your compass to the calculated radius and strike a full-circle arc with the compass point at the calculated center,

The equation of a circle centered at and with radius is:



John

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
formula for circle is:

%28x-h%29%5E2+%2B+%28y-k%29%5E2+=+r%5E2

(h,k) are the center of the circle.

r is the radius of the circle.

end points of your diameter are (-1,-7) and (5,10).

midpoint of that line is given by the equation:

midpoint of line = (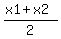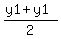%28x1%2Bx2%29%2F2 , %28y1%2By1%29%2F2)

since (x1,y1) = (-1,-7) and (x2,y2) = (5,10), this becomes:

midpoint of line = ((-1+5)/2),(-7+10)/2)) = (4/2,3/2) = (2,3/2).

formula for your circle should be %28x-2%29%5E2+%2B+%28y-%283%2F2%29%29%5E2+=+r%5E2

end points of the radius are:

(2,3/2) and (5,20)

length of the radius = 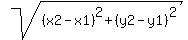sqrt%28%28x2-x1%29%5E2+%2B+%28y2-y1%29%5E2%29

this becomes:

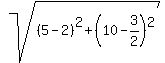
length of the radius = sqrt%28%285-2%29%5E2+%2B+%2810-3%2F2%29%5E2%29

this becomes:

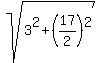
length of the radius = sqrt%283%5E2+%2B+%2817%2F2%29%5E2%29

this becomes:

length of the radius = .

since r+=+sqrt%2881.25%29, this means that r%5E2+=+81.25

formula for the circle is:

%28x-2%29%5E2+%2B+%28y-3%2F2%29%5E2+=+81.25

to graph this equation, we have to solve for y.

solving for y, we get:

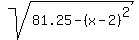
y+=+3%2F2 +/- sqrt%2881.25+-+%28x-2%29%5E2%29

graph of circle looks like this:



Answer by cov20(1) About Me  (Show Source):
You can put this solution on YOUR website!
The points(-1,-7) and (5,10) are the endpoints of the diameter of a circle. Graph the circle. Find an equation of the circle. Cordinates of Midpoint of diameter of a circle=((x1 x2)/2, (y1 y2)/2): ((-1 5)/2, (-7 10)/2)=(2, 3/2). Where a=2 and b=3/2, radius r^2 =(a-x1)^2 (b-x2)^2: r^2=(2--1)^2 (3/2--7)^2, r=9.01. Eqn of circle: (x-a)^2 (y-b)^2=r^2: (x-2)^2 (y-3/2)^2=81.25.