|
Question 1210191: What is the distance between the points (\cos 37^{\circ}, \sin 37^{\circ}) and (\cos 127^{\circ}, \sin 127^{\circ})?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the distance between the two points.
**1. Recall the Distance Formula**
The distance between two points (x₁, y₁) and (x₂, y₂) is given by:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
**2. Apply the Distance Formula**
In this case:
* (x₁, y₁) = (cos 37°, sin 37°)
* (x₂, y₂) = (cos 127°, sin 127°)
So, the distance is:
d = √((cos 127° - cos 37°)² + (sin 127° - sin 37°)²)
**3. Expand the Squares**
d = √(cos² 127° - 2cos 127° cos 37° + cos² 37° + sin² 127° - 2sin 127° sin 37° + sin² 37°)
**4. Use Trigonometric Identities**
* cos² θ + sin² θ = 1
* So, cos² 127° + sin² 127° = 1 and cos² 37° + sin² 37° = 1
d = √(1 + 1 - 2(cos 127° cos 37° + sin 127° sin 37°))
d = √(2 - 2(cos 127° cos 37° + sin 127° sin 37°))
**5. Apply the Cosine Difference Formula**
* cos(A - B) = cos A cos B + sin A sin B
* In our case, A = 127° and B = 37°
d = √(2 - 2cos(127° - 37°))
d = √(2 - 2cos(90°))
**6. Evaluate cos(90°)**
* cos(90°) = 0
d = √(2 - 2(0))
d = √2
**Therefore, the distance between the points is √2.**
Answer by ikleyn(53419)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the distance between the points (cos 37°, sin 37°) and (cos 127°,sin 127°)?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is a joking Math problem to solve it in 6 seconds mentally.
For it, notice that the difference 127° - 37° is 90°.
So, we have two intervals in the coordinate plane of the length 1 each,
emanated from the origin of the coordinate plane and perpendicular to each other.
The distance between their endpoints is the hypotenuse of a right angled triangle
and has the length 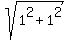 = =  . <<<---=== ANSWER . <<<---=== ANSWER
Solved.
-------------------------
It is a typical Math problem of Math mental competitions on solving Math problems quickly
in seconds, where the winner is a student who gives a correct answer quicker than others.
In such competitions, every second counts.
The winner is a student, who sees the simplest,
the shortest and the most straightforward/effective way to solve.
The same as at any professional job interview.
|
|
|
| |