|
Question 1203060: The vertices of a square are (-2,2),(3,4),(5,-1) and(0,-3).Find the coordinates of the center of the square.
Found 3 solutions by math_tutor2020, Edwin McCravy, ikleyn:
Answer by math_tutor2020(3821)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hint:
Label the four points as A,B,C,D
A = (-2,2)
B = (3,4)
C = (5,-1)
D = (0,-3)
This is what the diagram looks like

I used GeoGebra to make the diagram.
The goal is to find the location of point E.
One very useful property about squares is the diagonals bisect each other.
Bisect means "to cut in half".
Therefore, AE = EC and BE = ED.
The diagonals intersect to form the center.
This tells us that E is the midpoint of diagonal AC.
To go from A to C, we follow the pathway "down 3, right 7". Cut each of those values in half so we know how to go from A to E.
I'll let the student do this part.
Other methods are possible. One alternative is to find the equations of lines AC and BD.
Then use substitution or elimination to find the coordinates of point E.
The first method I mentioned is a faster route in my opinion.
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Standard procedure to find the geometric center of any regular polygon given by coordinates of its vertices
is to find the mean arithmetic of x-coordinates and the mean arithmetic of y-coordinates, separately.
It works for regular triangles, squares, pentagons, heptagons and all other regular " n-gons ".
In your case,  = = 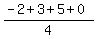 = 1.5; = 1.5;  = = 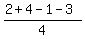 = 0.5. ANSWER = 0.5. ANSWER
It also works for arbitrary triangles, parallelograms, arbitrary quadrilaterals etc., when you look for the  of the figure. of the figure.
In addition to 2D, it works in 3D space for regular polyhedrons, too.
To learn more, see the lessons
- The Centroid of a triangle is the Intersection point of its medians
- The Centroid of a parallelogram is the Intersection point of its diagonals
in this site.
|
|
|
| |