SOLUTION: 1. Y=2x^2-5 2. Y=-3(x+1)^2+2. 3. y=1/2(x-2)^2-4 For each of these three separate quadratic equation find the Sketch: Doma

Algebra ->  Coordinate-system -> SOLUTION: 1. Y=2x^2-5 2. Y=-3(x+1)^2+2. 3. y=1/2(x-2)^2-4 For each of these three separate quadratic equation find the Sketch: Doma      Log On


   

Question 1194988: 1. Y=2x^2-5 2. Y=-3(x+1)^2+2. 3. y=1/2(x-2)^2-4 For each of these three separate quadratic equation find the

Sketch:
Domain:
Range
Direction of opening:
Vertex:
X-intercept;
Y-intercept:
Axis of symmetry:
Expansion/compression:
Congruent to:
MIN/MAX value:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

1. y=2x%5E2-5+
Sketch:
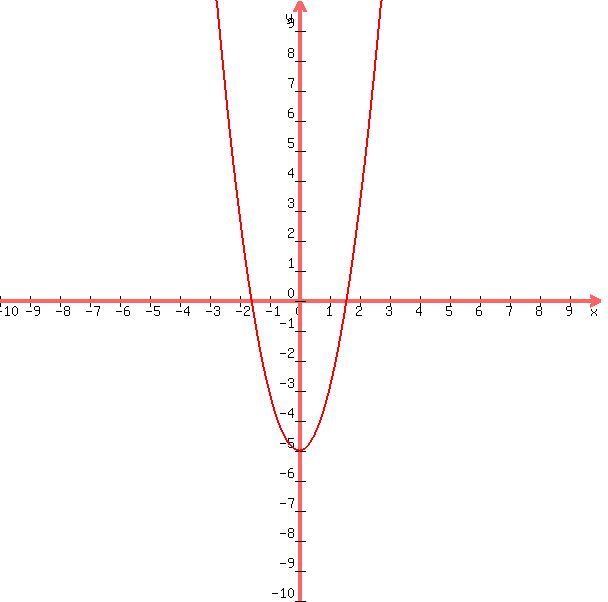
+graph%28600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+2x%5E2-5%29+
Domain: R (all real numbers)
Range:{ y element R+: y%3E=-5 }
Direction of opening: opening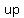+up
Vertex: (0, -5)
X-intercept:
set y=0
0=2x%5E2-5+
2x%5E2=5
x%5E2=5%2F2
x=sqrt%285%2F2%29 or x=-sqrt%285%2F2%29+
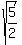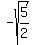so, X-intercept are at (sqrt%285%2F2%29, 0) and (-sqrt%285%2F2%29, 0)

Y-intercept: set x=0 =>y=-5+
and Y-intercept is at (0,-5)
Axis of symmetry: x=0
Expansion/compression: a stretch by a factor of 2 in y-direction
Congruent to: y=2%28x%5E2-5%2F2%29+
MIN/MAX value: minimum at (0,-5)


2. y=-3%28x%2B1%29%5E2%2B2

Sketch:
+graph%28600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+-3%28x%2B1%29%5E2%2B2%29+
Domain: R (all real numbers)
Range: { y element R : y%3C=2 }
Direction of opening: opening down
Vertex: (-1,2)
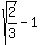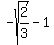X-intercept; -3%28x%2B1%29%5E2%2B2=0 at x+=+-sqrt%282%2F3%29-1 and x+=+sqrt%282%2F3%29+-+1
=>(sqrt%282%2F3%29+-+1,0) and (-sqrt%282%2F3%29-1,0)
Y-intercept: x=0, y=-3%280%2B1%29%5E2%2B2=-3%2B2=-1
=>(0,-1)
Axis of symmetry: x=-1
Expansion/compression: stretched by a factor of 3 in y-direction
Congruent to: y+=+-3+x%5E2+-+6+x+-+1
MIN/MAX value: max at (-1,2)


3. y=%281%2F2%29%28x-2%29%5E2-4+


Sketch:
+graph%28600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+%281%2F2%29%28x-2%29%5E2-4+%29+
Domain: R (all real numbers)
Range:{ y element R : y%3E=-4 }
Direction of opening: up
Vertex: (2,+-4)
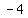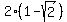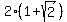X-intercept; ( 2%281+-+sqrt%282%29%29 ,0) and (2+%281+%2B+sqrt%282%29%29, 0)
Y-intercept: (0,-4)
Axis of symmetry: x=2
Expansion/compression: compressed by factor 2 in y-direction
Congruent to: y+=+x%5E2%2F2+-+2x+-+2
MIN/MAX value: minimum at (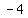2,+-4)