SOLUTION: The line y= -12/5 x + 2 is exactly 3 units away from two other lines parallel to it.The distance in units between the y-intercepts of these two other lines is.

Algebra ->  Coordinate-system -> SOLUTION: The line y= -12/5 x + 2 is exactly 3 units away from two other lines parallel to it.The distance in units between the y-intercepts of these two other lines is.      Log On


   

Question 1132638: The line y= -12/5 x + 2 is exactly 3 units away from two other lines parallel to it.The distance in units between the y-intercepts of these two other lines is.
Found 2 solutions by MathLover1, Boreal:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
The line y=-%2812%2F5%29+x%2B+2 is exactly 3 units away from two other lines parallel to it.
y=-%2812%2F5%29+x%2B+2...both sides multiply by 5
5y=-12+x%2B+10
12x+%2B+5y+-+10+=+0+

The distance from a point (x,+y) to a line ax+%2B+by+%2B+c+=+0 is given by
distance = ax+%2B+by+%2B+c%29%2Fsqrt%28a%5E2%2Bb%5E2%29+

You have the line
12x+%2B+5y+-+10+=+0+=>a=12,b=5,c=10

You want the distance from y-intercept point (0, y) to be 3.

%2812%2A0+%2B+5%2Ay+-+10%29%2Fsqrt%2812%5E2%2B5%5E2%29++=+3+
%285%2Ay+-+10%29%2Fsqrt%28169%29++=+3+
%285%2Ay+-+10%29%2F13+=+3+ ... multiply by 13
5%2Ay+-+10+=+39+
5%2Ay++=+39%2B10+
5%2Ay++=+49
y++=+49%2F5

This has two solutions:

+5y+-+10+=+39
+y+=+49%2F5+
And
+5y+-+10+=+-39+
+y+=+-29%2F5+

=> two other lines parallel to given line are:
y=-%2812%2F5%29+x%2B+49%2F5 and y=-%2812%2F5%29+x-29%2F5


In the graphic, the radius of the circle is 3, showing the distance to the other two lines is 3.

The difference of these two y-intercept values is
+49%2F5+-+%28-29%29%2F5+=+78%2F5+=+15.6+=>156%2F10=>153%2F5
answer: D)15+3%2F5


Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
The slope of the line is -12/5, and the slope of the line perpendicular to that is 5/12.
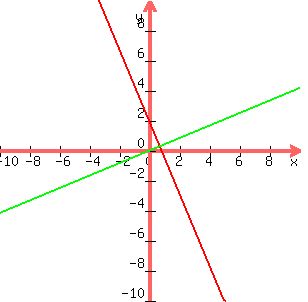
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C-2.4x%2B2%2C5x%2F12%29
this is the general form of the line perpendicular to the given line.
We want to go 3 units out on the perpendicular.
Suppose the perpendicular is to the line at the x-intercept of (5/6, 0). Then the line can be shown using the point slope formula of y-y1=m(x-x1), where m is slope and (x1, y1) are (5/6, 0) to be y=(5/12)x-(25/72)
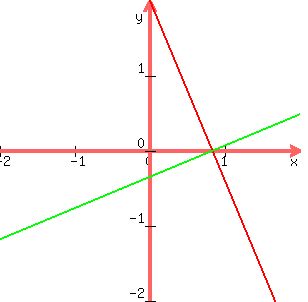
graph%28300%2C300%2C-2%2C2%2C-2%2C2%2C-2.4x%2B2%2C5x%2F12-%2825%2F72%29%29
Going to the right 3 units is a right triangle with the line 3 units away. The length of the hypotenuse is where the x-intercept is for that line. The angle for a slope of 5/12 is where the tangent of an angle is 5/12, which is arc tan (5/12) or 22.62 degrees.
So cos 22.62 =3/hypot
hypot=3/cos 22.62=3.25 units away from (5/6, 0) so the x-intercept of that line is 3.25+5/6 or (4.08, 0)
We know the slope of this parallel line is -2.4, and we have a point, so the equation of the line is y=-2.4(x-4.08)=y=-2.4x+9.08.
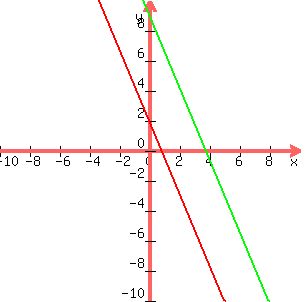
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C-2.4x%2B2%2C-2.4x%2B9.08%29
The distance to the x-intercept in the other direction is -3.25 units, so the x-intercept is at -3.25+5/6=-2.42 or (-2.42, 0)
The equation of this line is y=-2.4(x+2.42)=-2.4x-5.8
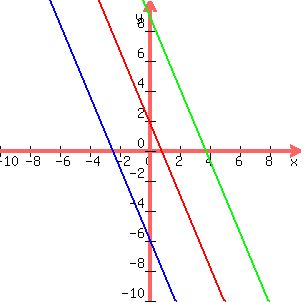
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C-2.4x%2B2%2C-2.4x%2B9.08%2C-2.4x-5.8%29
The distance between the two y-intercepts is 9.08-(-5.8)=14.88 units ANSWER