|
Question 1082351: Find the equation of a circle that its center is on the line x-2y-9=0 and passes through points (7,-2) and (5,0).
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39613)   (Show Source):
Answer by ikleyn(52750)  (Show Source):
You can put this solution on YOUR website! .
Find the equation of a circle  which has the center on the line x-2y-9=0 and passes through points (7,-2) and (5,0).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The locus of the points equidistant from two given points is the perpendicular bisector to the segment connecting these points.
So, you need to construct the perpendicular bisector to the segment connecting the given points
P = (7,-2) and Q = (5,0), and then find its intersection with the given straight line.
The midpoint between the two given points is (6,-1).
The segment connecting (7,-2) and (5,0) has the slope 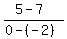 =  = -1.
Hence, the perpendicular line (perpendicular bisector) has the slope 1.
The line with the slope 1 passing through the point (6,-1) has the equation
y - (-1) = (1)*(x-6), or
y = x - 7.
The intersection of the straight lines
x - 2y - 9 = 0 (1) (the given line) and
y = x - 7 (2) (the perpendicular bisector)
is (solve the system by substitution) the point (x,y) = (5,-2)
So, the center of the circle is the point (5,-2).
|
|
The radius of the circle is the distance from the point (5,-2) to the point (5,0) is 2 units
Hence, the radius of the circle is 2.
Therefore, the equation of this circle is
 = 4.
The solution is completed.
Writing by "josgarithmetic" was ABSOLUTELY WRONG and TOTALLY IRRELEVANT until that moment when he saw my correct solution.
After getting my solution before his eyes, he quickly and quietly corrected his own (by simply rewriting my).
Simply ignore it. You will learn NOTHING reading his writings.
This problem is far above of his understanding and competency.
I am forced to use these not "completely polite" words, because he does not understand and doesn't want understand my regular and
conventional appeals to him.
|
|
|
| |
