|
Question 935859: p ↔ (p v q )
prove:q → p
Found 2 solutions by Theo, Edwin McCravy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! you set up a truth table for p, q, (p v q) and p <-> (p v q)
(p v q) is true if one of them is true.
(p v q) is false if both are false.
p <-> (p v q) is true if both have the same truth value.
p <-> (p v q) is false if both do not have the same truth value.
q -> p is false if q is true and p is false.
otherwise q -> p is true.
if the truth table for p <-> (q v p) is has exactly the same truth values as the truth table for q -> p, then they are equivalent.
the truth tables are shown below:
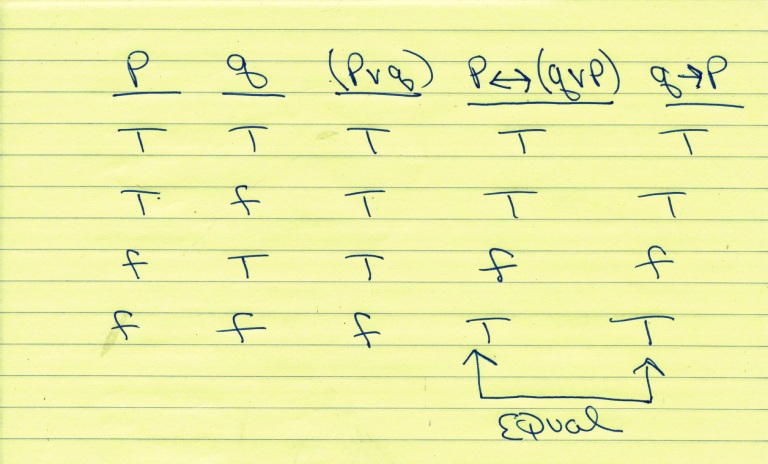
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website!
I'm sure your teacher didn't mean to use truth tables.
1. p ↔ (p v q )
prove:q → p
2. (p v q) → p 1,BE biconditional simplification, elimination
3. ~p → ~(p v q) 2,MT modus tollens
4. ~p → (~p & ~q) 3,DM DeMorgan's law
5. ~p → ~q 4,CS conjunctive simplification
6. ~~q → ~~p 5,MT modus tollens
7. q → p 6,DN double negation
Edwin
|
|
|
| |
