SOLUTION: Given that {{{ sqrt( 6.4*10^n ) }}} is a rational number, what can you say about the value of n? What if both {{{ sqrt( 6.4*10^n ) }}} and {{{ root(3, 6.4*10^n ) }}} are rational?

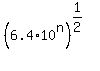
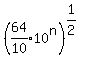
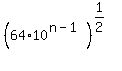
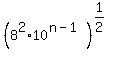
Only integer powers of 10 are rational. So the exponent
must be an integer, say k



n-1 = 2k

n = 2k+1

Therefore n must be odd in order that 
be rational.

For












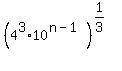
Only integer powers of 10 are rational. So the exponent
must be an integer, say p



n-1 = 3p

n = 3p+1

Therefore n must be 1 more than a multiple of 3

Now we set the exponents equal:

n = 3p+1 = 2k+1

3p = 2k

2p+p = 2k

p +  = 2k

 = 2k-p

The right side is an integer, so the left side must be also

Let that integer be A

Then 

 = A 

p = 2A

Substitute in

3p = 2k

3(2A) = 2k

6A = 2k

3A = k

Now supstitute in

n = 3p+1 = 2k+1

n = 3(2A)+1 = 2(3A)+1

n = 6A+1 = 6A+1 

So n must be 1 more than a multiple of 6.

Edwin