|
Question 1180016: Suppose you play poker with five of your friends every week, but you’re not very good. For every week you win, there are eight weeks where you lose. You don’t play for real money though, so it’s usually no big deal. But next week your friends want to have a real game where everyone puts in $15. The winner keeps all the money, everyone else loses their $15.
a)What is the expected monetary value of playing next week?
b)Now suppose you see a book that teaches people to improve their poker game. The book costs $30, but it will increase your odds of winning.
How much would the book have to increase your odds of winning to make the expected value of buying it positive?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)   (Show Source):
You can put this solution on YOUR website!
Part (a)
W = event that you win the game
P(W) = probability of winning
P(W) = 1/9
Since you win 1 week, but lose 8 weeks, so 1+8 = 9 weeks in total.
P(L) = probability of losing
P(L) = 1-P(W)
P(L) = 1-1/9
P(L) = 9/9-1/9
P(L) = (9-1)/9
P(L) = 8/9
V(W) = net value of winning
V(W) = (amount won) - (cost of playing)
V(W) = 15*(number of players) - 15
V(W) = 15*(you + five others) - 15
V(W) = 15*(1+5) - 15
V(W) = 15*6 - 15
V(W) = 90 - 15
V(W) = 75
You net $75 if you win
V(L) = net value of losing
V(L) = -15
Meaning you lost $15.
We'll multiply the probability values with the corresponding net values
P(W)*V(W) = (1/9)*(75) = 8.33 approximately
P(L)*V(L) = (8/9)*(-15) = -13.33 approximately
Add up the results:
8.33+(-13.33) = -5
On average, you should expect to lose about $5 per week. Because this value is not zero, this means the game is not mathematically fair.
Answer: -5 dollars
=====================================================================
Part (b)
Let's say the probability of winning any given week is P(W) = x.
That would mean P(L) = 1-x.
The net value of winning would be V(W) = 90-30 = 60, since you're spending $30 for the book.
Similarly, V(L) = 0-15-30 = -45. This is because you lose the $15 you bet in the game, on top of the $30 spent for the book. Overall, you lose $45.
We'll follow the same idea as before: multiply out the corresponding probability values with the net values, then add up the results
Multiply:
A = P(W)*V(W) = x*60 = 60x
B = P(L)*V(L) = (1-x)*(-45) = 45x-45
Add:
A+B = 60x+(45x-45) = 105x-45
This expression represents the expected value.
We want the expected value expression to be positive. So we want it to be larger than 0. Let's solve for x
105x - 45 > 0
105x > 45
x > 45/105
x > (3*15)/(7*15)
x > 3/7
This indicates that the probability x must be larger than 3/7 in order to have a positive expected value. Keep in mind that the largest x can get is x = 1. So we could be more careful and write  to express the full range of possible x values here.
Recall earlier that in part (a), the probability of winning was 1/9. This is without buying the book to improve your odds. We'll subtract 1/9 from 3/7 to get...
(3/7) - (1/9)
(27/63) - (7/63)
(27-7)/63
(27-7)/63
20/63
Going from a probability of 1/9 to 3/7 is an increase of 20/63. This is the amount the odds go up if you were to buy the book; assuming that we go for the smallest increase possible. To be more clear, the increase must be larger than this floor value to ensure that 105x-45 is positive.
In short, the book would have to increase your odds by at least 20/63 in order to get a positive expected value.
Answer: Increase by at least 20/63
Side note: 20/63 = 0.31746 approximately
Edit: My apologies, I did part (a) incorrectly earlier. I updated it to the correct solution however.
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
For part (a), I have different analysis and different answer.
Of every 9 games, you have one chance to win 15*6 = 90 dollars;
but you pay 15*9 = 135 dollars for 9 games.
Therefore, each game is worth  =  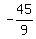= -5 dollars for you.
In other words, playing this game once every week, you lose statistically 5 dollars per game, in average.
-----------
I wrote this post to convince the other tutor to change his original solution.
|
|
|
| |
