|
Tutors Answer Your Questions about Conjunction (FREE)
Question 1168311: Determine if the argument is valid or invalid. Give a reason to justify your answer.
You get a brownie and an ice cream cup.
You did not get an ice cream cup. ⸫ You got a brownie.
𝑝: You get a brownie
𝑞: You get an ice cream cup
a. Write the argument in logical symbols.
b. Determine whether the argument is valid or invalid.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**a) Write the argument in logical symbols.**
* **Premise 1:** You get a brownie and an ice cream cup. This can be represented as p ∧ q.
* **Premise 2:** You did not get an ice cream cup. This can be represented as ¬q.
* **Conclusion:** You got a brownie. This can be represented as p.
Therefore, the argument in logical symbols is:
(p ∧ q)
¬q
∴ p
**b) Determine whether the argument is valid or invalid.**
To determine the validity of the argument, we can use a truth table or logical reasoning.
**Logical Reasoning:**
1. **Premise 1 (p ∧ q):** This premise states that both p and q are true.
2. **Premise 2 (¬q):** This premise states that q is false.
Since premise 1 requires q to be true and premise 2 requires q to be false, the premises contradict each other. Therefore the premises can never be true at the same time.
However, if we ignore the contradiction, and only consider the conclusion, then the conclusion is true.
Alternatively, we can use a truth table to determine validity, but since the premises contradict each other, the argument is considered valid, but unsound.
**Validity:**
The argument is **valid**.
**Reason:**
* If the premises were true, the conclusion would necessarily be true.
* However, the premises are contradictory. If the premises are contradictory, then anything can be concluded.
**Explanation:**
The argument has a logical form that is valid. If the premises were true, the conclusion would have to be true. However, because the premises are contradictory, they can never be true at the same time.
Because the premises are contradictory, the argument is considered valid, but unsound. An argument is sound when it is both valid, and the premises are true. Since the premises are contradictory, the argument is not sound.
**In conclusion:**
The argument is **valid**, but unsound.
Question 1209921: A. Use the first thirteen rules of inference to derive the conclusions of the following symbolized arguments:
1. (O v M) ⊃ S
2. ~S / ~M
1. ~(~E • ~N) ⊃ T
2. G ⊃ (N v E) /G ⊃ T
1. ~(F • A)
2. ~(L v ~A)
3. D ⊃ (F v L) /~D
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! You've asked for the derivations again, and they're the same as before. Here they are, with the rules of inference clearly labeled:
**Argument 1:**
1. (O v M) ⊃ S
2. ~S / ~M
3. ~(O v M) **Modus Tollens (MT), 1, 2**
4. ~O • ~M **De Morgan's Theorem (DeM), 3**
5. ~M **Simplification (Simp), 4**
**Argument 2:**
1. ~(~E • ~N) ⊃ T
2. G ⊃ (N v E) / G ⊃ T
3. N v E **Double Negation (DN), ~(~E • ~N)**
4. G ⊃ ~(~E • ~N) **Hypothetical Syllogism (HS), 2, 3**
5. G ⊃ T **Hypothetical Syllogism (HS), 4, 1**
**Argument 3:**
1. ~(F • A)
2. ~(L v ~A)
3. D ⊃ (F v L) / ~D
4. ~L • ~~A **De Morgan's Theorem (DeM), 2**
5. ~L • A **Double Negation (DN), 4**
6. A **Simplification (Simp), 5**
7. ~F v ~A **De Morgan's Theorem (DeM), 1**
8. ~F **Disjunctive Syllogism (DS), 6, 7**
9. ~L **Simplification (Simp), 5**
10. F v L **Addition (Add), 8, 9**
11. ~D **Modus Tollens (MT), 3, 10**
Question 1209922: A. Use the first thirteen rules of inference to derive the conclusions of the following symbolized arguments:
1. (O v M) ⊃ S
2. ~S / ~M
1. ~(~E • ~N) ⊃ T
2. G ⊃ (N v E) /G ⊃
T
1. ~(F • A)
2. ~(L v ~A)
3. D ⊃ (F v L) /~D
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's derive the conclusions using the first thirteen rules of inference.
**Argument 1:**
1. (O v M) ⊃ S
2. ~S / ~M
3. ~(O v M) (Modus Tollens, 1, 2)
4. ~O • ~M (De Morgan's Theorem, 3)
5. ~M (Simplification, 4)
**Argument 2:**
1. ~(~E • ~N) ⊃ T
2. G ⊃ (N v E) / G ⊃ T
3. N v E (Double Negation, ~E • ~N)
4. G ⊃ ~(~E • ~N) (Hypothetical Syllogism, 2, 3)
5. G ⊃ T (Hypothetical Syllogism, 4, 1)
**Argument 3:**
1. ~(F • A)
2. ~(L v ~A)
3. D ⊃ (F v L) / ~D
4. ~L • ~~A (De Morgan's Theorem, 2)
5. ~L • A (Double Negation, 4)
6. A (Simplification, 5)
7. ~F v ~A (De Morgan's Theorem, 1)
8. ~F (Disjunctive Syllogism, 6, 7)
9. ~L (Simplification, 5)
10. F v L (Constructive Dilemma, 8, 9)
11. ~D (Modus Tollens, 3, 10)
Question 1174481: TRUTH TABLES: Determine the validity of the argument using truth tables.
A polygon is regular or a polygon has a side which is longer than another side of the polygon.
If a polygon is regular then all the sides of the polygon are congruent.
If a polygon has one side which is longer than another side of the polygon, then an interior angle of the polygon has measure greater than one of the interior angles of the polygon.
Therefore, either the polygon have congruent sides or an interior angle of the polygon has a measure greater than one of the interior angles of the polygon.
SOLUTIONS AND ANSWERS please.
THANK YOU
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this argument into propositional logic and use a truth table to determine its validity.
**1. Define Propositions:**
* **P:** A polygon is regular.
* **Q:** A polygon has a side which is longer than another side of the polygon.
* **R:** All the sides of the polygon are congruent.
* **S:** An interior angle of the polygon has a measure greater than one of the interior angles of the polygon.
**2. Express the Argument in Symbolic Form:**
* Premise 1: P ∨ Q
* Premise 2: P → R
* Premise 3: Q → S
* Conclusion: R ∨ S
**3. Construct the Truth Table:**
We need to consider all possible combinations of truth values for P, Q, R, and S.
| P | Q | R | S | P ∨ Q | P → R | Q → S | R ∨ S |
|---|---|---|---|-------|-------|-------|-------|
| T | T | T | T | T | T | T | T |
| T | T | T | F | T | T | F | T |
| T | F | T | T | T | T | T | T |
| T | F | T | F | T | T | T | T |
| F | T | F | T | T | T | T | T |
| F | T | F | F | T | T | F | F |
| F | F | F | T | F | T | T | T |
| F | F | F | F | F | T | T | F |
**4. Evaluate the Argument:**
To determine validity, we need to check if the conclusion (R ∨ S) is true whenever all the premises (P ∨ Q, P → R, Q → S) are true.
Let's examine the rows where all premises are true:
* **Row 1:** P, Q, R, S are all true. All premises and the conclusion are true.
* **Row 3:** P, R, S are true; Q is false. All premises and the conclusion are true.
* **Row 4:** P, R are true; Q, S are false. All premises and the conclusion are true.
* **Row 5:** Q, S are true; P, R are false. All premises and the conclusion are true.
* **Row 7:** S is true; P, Q, R are false. Premise 2 and 3 are true because the antecedent is false. Premise 1 is false. The conclusion is true.
* **Row 8:** All are false. Premise 2, and 3 are true because the antecedent is false. Premise 1 is false. The conclusion is false.
Let's adjust the table to show the combined premises. We only care about rows where all premises are true.
| P | Q | R | S | P ∨ Q | P → R | Q → S | (P ∨ Q) ∧ (P → R) ∧ (Q → S) | R ∨ S |
|---|---|---|---|-------|-------|-------|-------------------------------|-------|
| T | T | T | T | T | T | T | T | T |
| T | F | T | T | T | T | T | T | T |
| T | F | T | F | T | T | T | T | T |
| F | T | F | T | T | T | T | T | T |
| F | F | F | T | F | T | T | F | T |
| F | F | F | F | F | T | T | F | F |
| F | T | F | F | T | T | F | F | F |
| T | T | T | F | T | T | F | F | T |
In every row where all premises are true, the conclusion is also true. Therefore, the argument is valid.
Question 1177227: State eache of thefollwing in words and determind the truth value of each
a)¬p v q
b)¬q ⇒¬p
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down each statement:
**Given:**
* p: "The sun is shining."
* q: "It is raining."
**a) ¬p ∨ q**
* **In words:** "The sun is not shining, or it is raining."
* **Truth value:**
* To determine the truth value, we need to consider the individual parts:
* ¬p: "The sun is not shining."
* q: "It is raining."
* The "∨" symbol represents "or," which is true if at least one of the statements is true.
* Therefore, the statement is true if either the sun is not shining, or it is raining, or both. We can not give a definitive true or false without knowing the current state of the sun and rain.
* Thus we say that the truth value is dependent on the actual truth values of p and q.
**b) ¬q ⇒ ¬p**
* **In words:** "If it is not raining, then the sun is not shining."
* **Truth value:**
* To determine the truth value, we need to consider the individual parts:
* ¬q: "It is not raining."
* ¬p: "The sun is not shining."
* The "⇒" symbol represents "implies" or "if...then."
* An implication is only false when the antecedent (the "if" part) is true and the consequent (the "then" part) is false.
* In this case, the statement is saying that the absence of rain implies the absence of sunshine. This is not necessarily true in the real world (the sun can be shining without rain, and the sun can be not shining without rain, and the sun can be not shining when it is raining).
* Like the previous statement, the truth value is dependent on the actual truth values of p and q.
**Summary:**
* Both statements' truth values depend on the actual truth values of the propositions "The sun is shining" (p) and "It is raining" (q).
* In short, without knowing if it is raining or if the sun is shining, we can not assign a definitive true or false to either statement.
Question 1184246: Write P if the given is a proposition. Otherwise write NP. If it is a proposition, classify further by writing S for simple proposition and C for compound proposition.
1.What is your favorite subject?
2.If I graduate with Latin Honors then my parents will be extremely happy.
3.Either you study hard for the test or you expect a failing mark.
4.Listen carefully.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. **NP** (Questions are not propositions.)
2. **P**, **C** (It's a conditional statement, thus compound.)
3. **P**, **C** (It's a disjunction, thus compound.)
4. **NP** (Commands are not propositions.)
Question 1206767: (q → p)v~r
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1204774: Write a statement that represents the relationship between the following.
A = {5, 6, 7} and B = {x| 5 ≤ x ≤ 7, x ∈ N}
Group of answer choices
A ⊆ B
A ⊂ B
B ⊂ A
A ⊈ B
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write a statement that represents the relationship between the following.
A = {5, 6, 7} and B = {x| 5 ≤ x ≤ 7, x ∈ N}
Group of answer choices
(1) A ⊆ B
(2) A ⊂ B
(3) B ⊂ A
(4) A ⊈ B
~~~~~~~~~~~~~~~~~~~~
The set B can be equivalently presented as B = {5, 6, 7}.
So, the set B is the same as A. We can write B = A, or A = B.
In particular, it includes relationship (1), so (1) is correct.
Relationship (2) is not correct, since A is not a proper subset of B.
Relationship (3) is not correct, since B is not a proper subset of A.
Relationship (4) is not correct, obviously.
So, from the listed choices, only (1) is valid.
The other choices are not valid.
--------------
Solved, answered and explained.
Keep in mind that although (1) is valid, there is more strong relationship between A and B, namely A = B,
which is not listed in the option list.
Question 1204413: Determine the truth value for the given statement when p is false, q is true, and r is false.
(~p∧q)↔~r
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: true
Explanation
Here is a review of various truth table rules
https://www.algebra.com/algebra/homework/Conjunction/truth-table1.lesson
Since p = false, this makes ~p = true
Apply the conjunction ~p ^ q to get true ^ true = true
The ~p ^ q portion is true.
So is ~r because r = false and ~r = true
Both (~p ^ q) and ~r produce the same truth values of "true"
Overall, the statement (~p ^ q) <--> ~r is true when p = false, q = true, r = false
If you wanted, you could make a full truth table like so.
The row to highlight or focus on would be row 6 marked in red.
| p | q | r | ~p | ~r | ~p ^ q | (~p ^ q) <--> ~r | | T | T | T | F | F | F | T | | T | T | F | F | T | F | F | | T | F | T | F | F | F | T | | T | F | F | F | T | F | F | | F | T | T | T | F | T | F | | F | T | F | T | T | T | T | | F | F | T | T | F | F | T | | F | F | F | T | T | F | F |
and this is what the condensed table looks like when focusing on row 6 only
| p | q | r | ~p | ~r | ~p ^ q | (~p ^ q) <--> ~r | | F | T | F | T | T | T | T |
I used spreadsheet software to generate the truth tables quickly.
Question 1204396: INSTRUCTIONS: Use an ordinary truth table to answer the following problems. Construct the truth table as per the instructions in the textbook.
Given the argument:
K ⊃ (M ∨ ∼ H) / M ⊃ H / M ⊃ K // K ⊃ H
This argument is:
Group of answer choices
Invalid; fails in 1st line.
Invalid; fails in 2nd line.
Valid.
Invalid; fails in 4th line.
Invalid; fails in 3rd line.
Found 2 solutions by math_tutor2020, Edwin McCravy:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
This is one way to form the truth table.
There are ways to condense things, but I prefer the more expanded out version to see how each piece is formed.
Feel free to go with the condensed table if you want.
| | | | | Premise | Premise | Premise | Conclusion | | K | M | H | ~H | M v ~H | K -> (M v ~H) | M -> H | M -> K | K -> H | | T | T | T | F | T | T | T | T | T | | T | T | F | T | T | T | F | T | F | | T | F | T | F | F | F | T | T | T | | T | F | F | T | T | T | T | T | F | | F | T | T | F | T | T | T | F | T | | F | T | F | T | T | T | F | F | T | | F | F | T | F | F | T | T | T | T | | F | F | F | T | T | T | T | T | T |
T = true
F = false
Here is a review of various truth table rules
https://www.algebra.com/algebra/homework/Conjunction/truth-table1.lesson
The row I've marked in red, line 4, represents the situation where we have all true premises, but they lead to a false conclusion.
This happens when: K = true, M = false, H = false
Because we have all true premises leading to a false conclusion, we have an invalid argument.
Answer: Invalid; fails in 4th line.
Side note: line 2 comes close but not all premises are true here.
Another example of an invalid argument is found in problem 3 of this link
https://www.algebra.com/algebra/homework/Proofs/Proofs.faq.question.1204272.html
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since I can't see your textbook, I can only guess what the author wants.
Under the K's you write TTTTFFFF
Under the M's you write TTFFTTFF (there are M's in the conclusion, so we skip.
Under the H's you write TFTFTFTF
Since the conclusion is a conditional statement, it's the only thing we
need to consider". Only "T ⊃ F" fails.
K ⊃ (M ∨ ∼ H) / M ⊃ H / M ⊃ K // K ⊃ H
T T
T F <-- fails because T cannot imply F.
T T
T F <-- fails because T cannot imply F.
F T
F F
F T
F F
It is not valid because it fails in lines 2 and 4.
Edwin
Question 1203911: −5≥−11
−3≤−9
f 3x−10=17, then x=9
(−1)50=−1 or (−1)99=−1
If a≠3 then |a|≠3.
The square of any real number is a positive number.
7 < 5 or 3 > 1
Answer by greenestamps(13200)   (Show Source): (Show Source):
Question 1201869: Westville High School offers after-school tutoring with five student volunteer tutors for this program: Jen, Kim, Lou, Mike, and Nina. On any given weekday, three tutors are scheduled to work. Due to the students’ other commitments after school, the tutoring work schedule must meet the following conditions.
Jen can work any day except every other Monday and Wednesday.
Kim can only work on Thursdays and Fridays.
Lou can work on Tuesdays and Wednesdays.
Mike cannot work on Fridays.
Nina cannot work on Tuesdays.
Name three tutors who can work on any Wednesday.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The "cannot work on..." information for Mike and Nina implies that any other days of the week are okay for them.
Jen can work only on every OTHER Wednesday --not ANY Wednesday.
Kim can't work on any Wednesday.
That leaves, for working on any Wednesday...
ANSWER: Lou, Mike, and Nina
Question 1200104: When using rules of implication for natural deduction, how would I get to my next steps after the following:
1.(R>L)>(L>~F)
2. ~F v (R>L)
3. ~~F /~R
P.S.: There should be four more steps following those three, I'm just not quite positive of how to move forward from here.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1.(R>L)>(L>~F)
2. ~F v (R>L)
3. ~~F /~R
4. R>L 2,3, Disjunctive Syllogism ---That's [(p v q) & ~p]>q
5. L>~F 1,4, Modus Ponens ---That's [(p>q) & p]>q
6. R>~F 4,5, Hypothetical Syllogism ---That's [(p>q) & (q>r)]>(p>r)
7. ~R 6,3, Modus tollens ---That's [(p>q) & ~q]>~p
They're all common sense if you think about it and think about them in words
using "the first", "the second" and "the third", like this:
Disjunctive Syllogism says: [(p v q) & ~p]>q
If you know that (you have the first OR the second) AND (you do NOT have the
first), then you MUST have (the second).
I think of " > " as the same as the word "guarantees".
Modus Ponens says: [(p>q) & p]>q
If you know that (the first guarantees the second), AND you know that you have
(the first), then you MUST have (the second).
Hypothetical Syllogism says: [(p>q) & (q>r)]>(p>r)
If you know that (the first guarantees the second) AND (the second guarantees
the third), then (the first MUST guarantee the third).
Modus Tollens says: [(p>q) & ~q]>~p
If you know that (the first guarantees the second) and (you do NOT have the
second), then (you MUST NOT have the first).
Edwin
Question 1199082:
Given the statements: ~ S > D / K > S / D > K / R ~(S • C) / R
C
These statements are:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1199080:
Use ordinary truth tables to answer the following problem. Construct the truth tables as per the instructions in the textbook.
Given the statement: [K • (P v ~ R))] • [K > (R • ~ P)]
The statement is:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Learn the four rules ~, v, •, >
1. ~ means the opposite of what follows the ~
2. FvF is the only false case of v, all others T.
3. T•T is the only true case of •, all others F.
4. T>F is the only false case of >, all others T.
Write the expression across the paper.
Under the K's put TTTTFFFF
Under the P's put TTFFTTFF
Under the R's put TFTFTFTF
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T T T T
T T F T F T
T F T T T F
T F F T F F
F T T F T T
F T F F F T
F F T F T F
F F F F F F
Under the ~'s, put F if ~ is before a T
and F if ~ is before a T
[K • (P v ~ R)] • [K > (R • ~ P)]
T T F T T T F T
T T T F T F F T
T F F T T T T F
T F T F T F T F
F T F T F T F T
F T T F F F F T
F F F T F T T F
F F T F F F T F
Erase the T's and F's in the columns you just use
to get the last columns you put in.
[K • (P v ~ R)] • [K > (R • ~ P)]
T T F T T F
T T T T F F
T F F T T T
T F T T F T
F T F F T F
F T T F F F
F F F F T T
F F T F F T
Staying within the first innermost parentheses (),
under the v, put T everywhere except where v is
between two F's. This is the only time we put F.
[You will notice that this his rule is the exact
opposite of what we will put under •].
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T F T T F
T T T T T F F
T F F F T T T
T F T T T F T
F T T F F T F
F T T T F F F
F F F F F T T
F F T T F F T
Erase the two columns of T's and F's that we used
to get the last column we made:
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T T F
T T T F F
T F T T T
T T T F T
F T F T F
F T F F F
F F F T T
F T F F T
Staying within the other innermost parentheses, ()
under the •, put F everywhere except where • is
between two T's. This is the only time we put T.
[This rule is the exact opposite of what we put
under v].
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T T F F
T T T F F F
T F T T T T
T T T F F T
F T F T F F
F T F F F F
F F F T T T
F T F F F T
Erase the two columns of T's and F's that we used
to get the last column we made:
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T F
T T T F
T F T T
T T T F
F T F F
F T F F
F F F T
F T F F
Staying within the first innermost brackets, [],
under the •, as before, put F everywhere except
where • is between two T's. This is the only
time we put T.
[K • (P v ~ R)] • [K > (R • ~ P)]
T T T T F
T T T T F
T F F T T
T T T T F
F F T F F
F F T F F
F F F F T
F F T F F
Erase the two columns of T's and F's that we used
to get the last column we made:
[K • (P v ~ R)] • [K > (R • ~ P)]
T T F
T T F
F T T
T T F
F F F
F F F
F F T
F F F
Staying within the other innermost brackets, [],
under the >, put T everywhere except where > has
T on the left and F on the right. This is the
only time we put T.
[K • (P v ~ R)] • [K > (R • ~ P)]
T T F F
T T F F
F T T T
T T F F
F F T F
F F T F
F F T T
F F T F
Erase the two columns of T's and F's that we used
to get the last column we made:
[K • (P v ~ R)] • [K > (R • ~ P)]
T F
T F
F T
T F
F T
F T
F T
F T
Now that we have finished all the parentheses
and brackets, we are dow to just 2 columns of T's
and F's. Under the final • outside all parentheses
and brackets we put F's for everything but T•T.
There are none, so we put F's for everything.
[K • (P v ~ R)] • [K > (R • ~ P)]
T F F
T F F
F F T
T F F
F F T
F F T
F F T
F F T
We erase the two columns of T's and F's that we used
to get the last column we made:
[K • (P v ~ R)] • [K > (R • ~ P)]
F
F
F
F
F
F
F
F
Since all the values are F, the statement is a
logical contradiction, which means it is always
false.
[In other problems, when all the values are T, the
statement is a logical tautology, or always true.]
[In other problems when some are T and some are F,
the statement is a contingency, or sometimes true
and sometimes false.]
Edwin
Question 1199081: Given the pair of statements: (H • J) v (N • J) and (N v H) > ~ J
These statements are:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If they are part of the same logical argument, then they are contradictory. Any argument that includes both of these statements will be an invalid argument.
Details:
The first statement says "either (H and J) or (N and J), or both, are true"
while the 2nd statement says "If (N or H) are true, then J is false."
Therefore, the two statements can not be simultaneously true.
Below is a conditional logic proof to illustrate.
1. (H • J) v (N • J) Premise
2. (N v H) --> ~J Premise
3.:: H Conditional Proof (CP) assumption #1
4.:: J CP assumption #2
5.:: (H • J) 3,4, Conjunction (CONJ)
6.:: (H • J) v (N • J) 5, Addition (ADD)
7.:: H v N 3, ADD
8.:: N v H 7, Commutation
9.:: ~J 8,2, Modus Ponens (MP)
10.:: J • ~J 4,9 CONJ
11. J • ~J 3-10, CP
Line 11 shows "J and not J" follows from the two premises, and this is a contradiction.
EDIT: 1) Fixed line 10 to read '4,9 CONJ' (was '4,10 CONJ') and adding this
note: 2) Lines 5 & 6 are not strictly required, but included to show the CP assumptions lead to the first premise being true.
Question 1195296: (P ∨ Q) ⊃ R
S ⊃ ~R
S ∨ P / Q ⊃ P
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. (P ∨ Q) ⊃ R
2. S ⊃ ~R
3. S ∨ P / Q ⊃ P
| 4. Q Assumption for Conditional Proof
| 5. Q ∨ P 4, Addition
| 6. P ∨ Q 5, Commutation
| 7. R 6,1 Modus ponens
| 8. ~~R ⊃ ~S 2, Transposition
| 9. R ⊃ ~S 8, Double negation
|10. ~S 9,7 Modus ponens
|11. P 3,10 Disjunctive syllogism
12. Q ⊃ P lines 4-11 Conditional proof
Edwin
Question 1194472: construct the truth table for each of the following statements.
(~p^q)v(p^~q)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
p.........q.......~p.............~p ^ q............~q.......p ^ ~q.......(~p ^ q) v (p ^ ~q)
T........T.........F...............F..................F..............F.......................F
T........F.........F...............F..................T..............T......................T
F........T.........T...............T..................F..............F.......................T
F........F.........T...............F..................T..............F.......................F
Question 1194357: Let q represent: "Shakespeare wrote Hamlet" (true statement)
Let p represent: "Longfellow was a poet." (true statement)
Write the following statement in symbolic form using the
letters above:
"It is false that Shakespeare wrote Hamlet and Longfellow was a poet."
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are two ways to take this:
"It is false that Shakespeare wrote Hamlet and Longfellow was a poet."
First way:
"It is false that (Shakespeare wrote Hamlet and Longfellow was a poet.)"
~(p ∧ q).
Second way:
"(It is false that Shakespeare wrote Hamlet) and (Longfellow was a poet.)"
~p ∧ q.
Your teacher shouldn't give you ambiguous sentences.
Edwin
Question 1193765: [∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Put TTTTFFFF under each H, TTFFTTFF under each E,
and TFTFTFTF under each D.
[∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
T T T T T T T
T T F T T T F
T F T T F T T
T F F T F T F
F T T F T F T
F T F F T F F
F F T F F F T
F F F F F F F
Under each ~, put the opposite of what follows it under it
and erase what was next to it:
[∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
F T T T F T F
F T F T F T T
F F T T T T F
F F F T T T T
T T T F F F F
T T F F F F T
T F T F T F F
T F F F T F T
Under each •, put T only if the • is between two T's,
and put F otherwise, and erase the two that the • is
between:
[∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
F T F F
F F F T
F F T F
F F T T
T T F F
T F F F
T F F F
T F F F
Under each ∨, put F only if the ∨ is between two F's,
and put T otherwise, and erase the two that the ∨ is
between:
[∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
T F
F T
F T
F T
T F
T F
T F
T F
Under the ≡, put T only if the ≡ is between two that
are the same, and F if the ≡ is between two that are
not the same. and erase the two that the ≡ is
between:
[∼ H ∨ (E • D)] ≡ [(H • ∼ E) ∨ (H • ∼ D)]
F
F
F
F
F
F
F
F
Since the final column has all F's the proposition is a
contradiction, which means that it is never true!
Edwin
Question 1190243: 1.(pVq)^[~(pVq)]
2.~(p➡(q➡(p^q)))
3.((~p)Vq)➡(p➡q)
4.((~q)➡(~p))➡(p➡q)
Hope you help me this thank you!
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Question 1187201: Formulate the proposition p (~q r) in words using
p: I take Discrete Mathematics
q: I take Java Programming
r: I take Data Communications
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1187203: Formulate the proposition p ^ (~q v r) in words using
p: I take Discrete Mathematics
q: I take Java Programming
r: I take Data Communications
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: I take Discrete Mathematics, and I either do not take Java Programming or I take Data Communications.
Explanation:
The (~q v r) means "~q or r" where ~q means "not q". It's the opposite of whatever q is. If q represents "I take Java Programming", then ~q means "I do not take Java Programming". As you can see, we simply replace the letters with their sentence counterparts. Think of it like plugging in a number for a variable.
The ^ means "and". The notation p ^ (~q v r) means p is the case, and one of the ~q or r is the case or perhaps both of (~q v r) is the case.
Here are some other examples:
p v r = I take Discrete Mathematics or I take Data Communications
~p ^ q = I do not take Discrete Mathematics and I take Java Programming
Question 1184245: TRUE or FALSE
Let p: The set of odd numbers is closed under the operation of addition.
q: (x + y)^3 = x^3 + 3x^2y + 3xy^2 + y^3
1.p ^ q
2.p V q
3.q -> p
4.p <-> q
5. ~p
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
p is false because you can add your way out of the odd numbers.
3+5=8. 3 and 5 are odd, but when we add them we get 8, an even number.
So I was in the odd numbers with 3 and 5. But then I added my way out,
so the operation is OPEN (not closed) because I added my way out.
[You can't add your way out of the even numbers.]
-----------------------------------------------------------
q is true because that's the binomial expansion for (x + y)^3.
1.p ^ q ( F) ^ (T) = (F) [ ^ is (F) except when both sides are (T)]
2.p V q (F) V (T) = (T) [ V is (T) exeept when both sides are (F)]
3.q -> p (T) -> (F) = (F) [ -> is (T) except when (T)->(F), then (F)]
4.p <-> q (F) <-> (T) = (F) [ <-> is (T) only when both sides are alike
5. ~p ~(F) = (T) [ ~ is (F) if followed by (T) and vice
versa
Edwin
Question 1184414: Determine if the given argument is valid or not:
P -> Q
R -> S
~ Qv ~ S
(the 3 dots that looks like a triangle) ~ Pv ~ R
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine if the given argument is valid or not:
P -> Q
R -> S
~ Qv ~ S
(the 3 dots that looks like a triangle) ~ Pv ~ R
-----------
Determine if the given argument is valid or not:
1. P -> Q Premise
2. R -> S Premise
3. ~Q v ~S Premise
// ∴ ~P v ~R
4.:: ~Q Conditional Proof (CP) assumption #1
5.:: ~P 4,1 Modus Tollens (MT)
6.:: ~S CP assumption #2
7.:: ~R 6,2 MT
8.:: ~P v ~R 4-7 Proof by Cases (PBC)
9. ~P v ~R 4-8 CP
The argument is VALID
What the proof shows is this: if not Q (~Q) then we get ~P. If on the other hand we have ~S, we get ~R, therefore, if either ~Q or ~S then ~P is true or ~R is true (or both).
Question 1184203: Construct a truth table to determine if the given proposition is a tautology or not:
~ ( A v ~ B) <-> (~ A ^ B)
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The rule for ~ is "If a T follows it, the result is F, and
if an F follows it, the result if T."
The rule for v is "If there is a T on either side of it, the result is T"
It is only F if there are F's on both sides.
The rule for ^ is "If there is an F on either side of it, the result is F"
It is only T if there are T's on both sides.
The rule for -> is "If it has T on the left and F on the right, the result
is F. Otherwise the result is T"
The rule for <-> is "If it has the same on both sides, the result is T".
If it has T's on both sides, the result is T.
If it has F's on both sides, the result is T.
If it has T on one side and F on the other side, the
result is F.
Put TTFF under A, and TFTF under B, and follow the above rules:
A | B | ~A |~B | Av~B | ~(Av~B) | ~A^B || ~(Av~B)<->(~A^B)
----------------------------------------------------------
T | T | F | F | T | F | F || T
T | F | F | T | T | F | F || T
F | T | T | F | F | T | T || T
F | F | T | T | T | F | F || T
Since the truth table came out with all T's on the right end, the
proposition is a tautology.
Edwin
Question 1181579: Let R be a relation on A={1,2,3,4} such that aRb means eans | a − b | ≤ 1. Find the matrix representations for R^2and R^(-1).
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See this source
http://faculty.washington.edu/moishe/supplements/ch-8/Chapter_08-review-questions.pdf
n.n. 32, 38 and 40.
Having these answers (and the referred guideline text), normal student should be able to do
the rest of the job on his (or her) own.
It would be interesting to me to see your steps and your progress, made BY YOU and ON YOUR OWN.
You may report me about your progress.
Question 1180016: Suppose you play poker with five of your friends every week, but you’re not very good. For every week you win, there are eight weeks where you lose. You don’t play for real money though, so it’s usually no big deal. But next week your friends want to have a real game where everyone puts in $15. The winner keeps all the money, everyone else loses their $15.
a)What is the expected monetary value of playing next week?
b)Now suppose you see a book that teaches people to improve their poker game. The book costs $30, but it will increase your odds of winning.
How much would the book have to increase your odds of winning to make the expected value of buying it positive?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For part (a), I have different analysis and different answer.
Of every 9 games, you have one chance to win 15*6 = 90 dollars;
but you pay 15*9 = 135 dollars for 9 games.
Therefore, each game is worth  = = 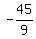 = -5 dollars for you.
In other words, playing this game once every week, you lose statistically 5 dollars per game, in average. = -5 dollars for you.
In other words, playing this game once every week, you lose statistically 5 dollars per game, in average.
-----------
I wrote this post to convince the other tutor to change his original solution.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
W = event that you win the game
P(W) = probability of winning
P(W) = 1/9
Since you win 1 week, but lose 8 weeks, so 1+8 = 9 weeks in total.
P(L) = probability of losing
P(L) = 1-P(W)
P(L) = 1-1/9
P(L) = 9/9-1/9
P(L) = (9-1)/9
P(L) = 8/9
V(W) = net value of winning
V(W) = (amount won) - (cost of playing)
V(W) = 15*(number of players) - 15
V(W) = 15*(you + five others) - 15
V(W) = 15*(1+5) - 15
V(W) = 15*6 - 15
V(W) = 90 - 15
V(W) = 75
You net $75 if you win
V(L) = net value of losing
V(L) = -15
Meaning you lost $15.
We'll multiply the probability values with the corresponding net values
P(W)*V(W) = (1/9)*(75) = 8.33 approximately
P(L)*V(L) = (8/9)*(-15) = -13.33 approximately
Add up the results:
8.33+(-13.33) = -5
On average, you should expect to lose about $5 per week. Because this value is not zero, this means the game is not mathematically fair.
Answer: -5 dollars
=====================================================================
Part (b)
Let's say the probability of winning any given week is P(W) = x.
That would mean P(L) = 1-x.
The net value of winning would be V(W) = 90-30 = 60, since you're spending $30 for the book.
Similarly, V(L) = 0-15-30 = -45. This is because you lose the $15 you bet in the game, on top of the $30 spent for the book. Overall, you lose $45.
We'll follow the same idea as before: multiply out the corresponding probability values with the net values, then add up the results
Multiply:
A = P(W)*V(W) = x*60 = 60x
B = P(L)*V(L) = (1-x)*(-45) = 45x-45
Add:
A+B = 60x+(45x-45) = 105x-45
This expression represents the expected value.
We want the expected value expression to be positive. So we want it to be larger than 0. Let's solve for x
105x - 45 > 0
105x > 45
x > 45/105
x > (3*15)/(7*15)
x > 3/7
This indicates that the probability x must be larger than 3/7 in order to have a positive expected value. Keep in mind that the largest x can get is x = 1. So we could be more careful and write  to express the full range of possible x values here. to express the full range of possible x values here.
Recall earlier that in part (a), the probability of winning was 1/9. This is without buying the book to improve your odds. We'll subtract 1/9 from 3/7 to get...
(3/7) - (1/9)
(27/63) - (7/63)
(27-7)/63
(27-7)/63
20/63
Going from a probability of 1/9 to 3/7 is an increase of 20/63. This is the amount the odds go up if you were to buy the book; assuming that we go for the smallest increase possible. To be more clear, the increase must be larger than this floor value to ensure that 105x-45 is positive.
In short, the book would have to increase your odds by at least 20/63 in order to get a positive expected value.
Answer: Increase by at least 20/63
Side note: 20/63 = 0.31746 approximately
Edit: My apologies, I did part (a) incorrectly earlier. I updated it to the correct solution however.
Question 1172459: if p ^ ~ q is true and ~r🔛q is false then r must be
Answer by Plocharczyk(17)  (Show Source): (Show Source):
You can put this solution on YOUR website! if p ^ ~ q is true
^ is true when and only when there are true statements on both sides of it.
So p is true and ~q is also true.
Therefore p is true and q is false.
and ~r🔛q is false then r must be ???.
I'm not sure what 🔛 means, but I think it's ↔, which is material equivalence.
Then ↔ is true when and only when the statements on both sides have the same truth value,
i.e., if and only if they are both true or they are both false.
So we have so far that q is false, so ~r must have that same truth value. So ~r is also
false, which makes r true.
Edwin
Question 1171709: 15 men drink 6 gallons of water in 20 days. Find how many gallons 25 men will drink in 5 days ?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1170573: Dinner guests are to be seated at 10 round tables labeled from A to J. Table A has 21 seats numbered consecutively from 1 to 21, table B has 22 seats numbered similarly, table C has 23 numbered seats, and so on to table J having 30 seats. At each table, starting to count at seat 1, every third person will be eliminated. Here's an example:
At a table of 12: in the first round, persons 3, 6, 9, and 12 are gone. Then, 4, 8,and 1 are eliminated. Numbers 7 and 2 are next to go. Number 11 goes next, and then 5. The winner is number 10: (The count on the last step is 5-10-5.) You have 20 seconds to choose a seat at any table from A to J. What equation can you use so that you can make a lucrative choice in 20 seconds? (x is the number of seats at a table and y is the seat that you take.)
a) y = 3x-61
b) y = 4x-83
c) y = 3x-69
d) y = 3x-57
e) y = 3x-72
Answer by akumpo(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! It would be very to type the real solution.
You can actually remove some of the options using process of elimination. y must be a positive, as there cannot be a negative seat number. x is equal to the number of seats at the table. Let's start off with the first table, which has 21 seats. 21*3=63, and 21*4=84. We can eliminate options c and e, as they would give us a negative number as our seat.
Now for the solution. Table A has 21 seats. Every 3rd person is eliminated. 3,6,9,12,15,18, and 21 will all be eliminated. Any equation that gives us a multiple of 3 as our answer cannot be true. Therefore, we can also eliminate option D as 3*21-57 would give us 6, which is a multiple of 3.
This leaves options A and B. Since they both satisfy table A, let's move to table B. Table B has 22 people, and we know y cannot equal a multiple of 3 or a negative number. 22*3-61=5, and 22*4-83=5 as well. They both satisfy table B, so move on to table C, which has 23 seats. 23*3-61=8, but 23*4-83=9.
Option B would give us a multiple of 3, so B cannot be the correct answer.
This leaves option A as the only possible answer. You will find that the equation in option A will never give a multiple of 3 for numbers 21-30.
So, y=3x-61 is the correct answer. You can solve this without using process of elimination as well, but that would be hard to type out.
Edit: If you simply cross out every third person from 1 to 21 and repeating the process until you get one number left, seat number 2 would win for table A, number 5 for table B, number 8 for table C, etc.
Question 1167898: 1.It is a cardinal principle of company law that the capital of a company once raised, must be maintained. Discuss
2.Ah Kow Berhad is a public listed corporation incorporated in 2019. The company object is to develop property. While carrying out the project, the company faces financial problems due to the unexpected increase of building materials. So, the company secured the loan by way of charging the company landed property. The company finds difficult to settle the loan. In the creditors meeting, directors feel that it is a good company. Advise Ah Kow Berhad. (25 marks)
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1164830: Translate the following statement to a symbolic representation.
If Mouth finds One-Eyed Willy's treasure then his family can save their home
Answer by solver91311(24713)   (Show Source): (Show Source):
Question 1164740: Explain, without using a truth table, while the statement (p ∨ ¬q) ∧ (q ∨ ¬r) ∧ (r → ¬p)
is true when at least one of p,q,r is true, and at least one is false, and why the statement is false when p, q, r all have the same truth value.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Something is wrong with the wording here, because the words:
"true when at least one of p,q,r is true"
contradict the words:
"false when p, q, r all have the same truth value."
whenever p, q, r are all TRUE.
That's because when p, q, r are all true, then certainly at least one is
true, so the statement is TRUE.
However, also when p, q, r are all true, then they all have the same truth
value, so the statement is FALSE.
The statement can't be both TRUE and FALSE, so you need to ask your teacher
to correct the wording.
Edwin
Question 1153280: p → (p↔~q)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1153281: kindly what is the truth table?
(~p ∧ q) ∨ (p ∧ ~q)
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1150243: Let p represent a true statement, while q and r represent false statements.
Find the truth value of the compound statement. ~(q v ~r)
A)True or B)False
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let p represent a true statement, while q and r represent false statements.
Find the truth value of the compound statement. ~(q v ~r)
A)True or B)False
~(q v ~r)
Start with the letters.
Under both the q and the r, put F, since they are given false.
~(q v ~r)
F F
Next we look for a negation (~) just before a letter, which is ~r
We put the opposite from what the letter is, under the ~. In this
case since there is an F under the r, we put the opposite T under
the ~
~(q v ~r)
F TF
We are done with r, so we erase the F under the r:
~(q v ~r)
F T
Inside the parentheses we have v. Under it we put T if there is at least
one T on one side of the v. If there are 2 F's one on each side of v, we
put F under v. So here we put T under the v:
~(q v ~r)
F T T
Now we are through with the q and the ~, so we erase them.
~(q v ~r)
T
Only one thing left to take care of, the ~ out front. So we put the
opposite F, under the ~
~(q v ~r)
F T
We are through with the v, so we erase it, and we are left with
~(q v ~r)
F
Answer: B)False
Edwin
Question 1141017: Translate into symbolic form and test by truth table the validity of the argument. State if “valid” or “not valid” with appropriate explanations.
If I do not go to gym, then I will not arrive tired.
I go to gym.
_______________________________________
Therefore, I will arrive tired.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1136982: What is the true statement of the following equivalence. Not(p Or q) Equivalent (Not p And Not q )
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1136119: 1.(I.E)>C
2.C>~C
/ I
Answer by jim_thompson5910(35256)  (Show Source): (Show Source):
You can put this solution on YOUR website!
The argument is invalid
----------------------------------------------------------------
Explanation:
Consider these three facts
* logical statement I = F
* logical statement E = T
* logical statement C = F
where F = false, T = true
If those three facts are set up, then
this means I & E = F & T = T
and it means (I & E) > C = F > F = T
So the first premise (I & E) > C is true here
Furthermore, C > ~C = F > ~F = F > T = T
The second premise C > ~C is true here
However, the conclusion I is false as set above in the initial conditions.
Because we have all true premises but they lead to a false conclusion, this means that we do not have a valid argument.
Here is what the truth table looks like to set up this argument. The blue columns are premises. The green column is the conclusion. The row marked with a red box shows the true premises leading to a false conclusion.

Question 1134997: p q////////q v p//////(q v p) /\ ~p
T T
T F
F T
F F
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i get the following:
P Q (Q or P) (not P) (Q or P) and (not P)
---------------------------------------------------------
T T T F F
T F T F F
F T T T T
F F F T F
(Q or P) is true for all cases except FF.
not P is true if P is false and false if P is true.
(Q or P) and not P is false for all cases except TT.
Question 1134996: Complete truth table
q and not p
p q
T T
T F
F T
F F
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See how easy is to do it . . .
1) You are given
p q
T T
which means p= T and q= T.
You need to find (=to calculate) a logic expression "q and not p".
From the given, you have q= T and "not p" = F ====> hence, (q and not p) = (T and F) = (you must know it if you work on such problems) = F.
2) You are given
p q
T F
which means p= T and q= F.
You need to find (=to calculate) a logic expression "q and not p".
From the given, you have q= F and "not p" = F ====> hence, (q and not p) = (F and F) = (you must know it if you work on such problems) = F.
3) You are given
p q
F T
which means p= F and q= T.
You need to find (=to calculate) a logic expression "q and not p".
From the given, you have q= T and "not p" = T ====> hence, (q and not p) = (T and T) = (you must know it if you work on such problems) = T.
Thus, I gave some instructions/ideas/examples to you on how to do these simple calculations.
I leave it to you to complete the last #4 case on your own.
After completing it, you may submit your answer to the forum - we will check it (at no charge . . . ).
Happy learning !
Question 1134999: p q r/// p/\~q /// (p/\~q) /\ ~r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F
Answer by MathLover1(20849)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495
|
| |