|
Question 935226: A conical cup is filled with icecream .The icecream forms a hemispherical shape on its open top.The height of the hemispherical part is 7 Cm.The radius of the hemispherical part equals the heighr of the cone .Then find the volume of the icecream is is ??
plz help me out.
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have a hemisphere connected to a cone, radius 7 cm, and cone height 7 cm, so you want the total volume of the hemisphere and cone.
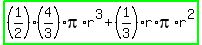 and you know r. and you know r.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I expect that what is mean is that the cone looks like this:
 That means the radius of the hemisphere, the radius of the cone, and the height of the cone are all 7 cm. That means the radius of the hemisphere, the radius of the cone, and the height of the cone are all 7 cm.
The volume of a sphere of radius  is is 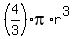 , and the volume of half a sphere is , and the volume of half a sphere is  of that. of that.
So the volume of the hemispherical (half a sphere) top part, in cubic centimeters, is
 . .
A cone of radius  and height and height  has a volue of has a volue of  , ,
so the volume of the conical bottom part, in cubic centimeters, is
 . .
The volume, in cubic centimeters, of the whole thing is the sum of the volumes of top and bottom parts:
 (rounding, and using 3.1416 for (rounding, and using 3.1416 for  ). ).
|
|
|
| |