|
Question 1198554: The area of a base of a cone is two-thirds the area of a base of a cylinder and their volumes are equal. Find the ratio of their altitudes.
Found 2 solutions by Shin123, math_tutor2020:
Answer by Shin123(626)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the radius of the cone be  , the radius of the cylinder be , the radius of the cylinder be  , the height of the cone , the height of the cone  , and the height of the cylinder , and the height of the cylinder  . Then, we have the equation . Then, we have the equation  . Our goal is to find . Our goal is to find 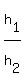 . First, we can divide . First, we can divide  from both sides to get from both sides to get  . We can multiply both sides by 3, then divide both sides by . We can multiply both sides by 3, then divide both sides by 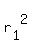 to get to get  . Dividing both sides by . Dividing both sides by  , we get , we get 
Since we know that the base of the cone is two-thirds the area of the base of the cylinder, we have the equation  . Dividing both sides by . Dividing both sides by  , we get , we get  . Multiplying both sides by . Multiplying both sides by  , we get , we get  . Finally, dividing both sides by . Finally, dividing both sides by 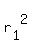 gives us gives us  . We can plug this into the first equation to get . We can plug this into the first equation to get  . .
The question doesn't state whether you want the ratio of the height of the cone over the height of the cylinder (which was what I derived), or the ratio of the height of the cylinder over the height of the cone. If you want that, the answer would instead be  . .
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
VL = volume of cylinder
VC = volume of cone
VC = VL since we're told these particular cone and cylinder have equal volume.
HL = height of the cylinder
HC = height of the cone
AL = area of the cylinder circular base
AC = area of the cone circular base
AC = (2/3)*AL
VL = (area of base)*(height)
VL = (AL)*(HL)
VC = (1/3)*(area of base)*(height)
VC = (1/3)*(AC)*(HC)
VC = (1/3)*((2/3)*AL)*(HC)
VL = (2/9)*AL*HC
(AL)*(HL) = (2/9)*AL*HC
HL = (2/9)*HC
HL/HC = 2/9
HC/HL = 9/2
The ratio of the cone's height (HC) over the cylinder's height (HL) is 9/2.
|
|
|
| |