SOLUTION: Three spherical planets of radius r are on orbits that keep them within viewing distances of one another. At any instant, each planet has a region that cannot be seen from anywhere

Let start considering TWO spherical planets. Let the points A and B be their centers.

Will call the planets A and B, using the same letters as their centers.


Consider the straight line AB. Then it is easy to understand what are unseen parts 
(regions) of each planet, that can not be seen from anythere of the other planet.

This region for planet B is the "rear" hemi-sphere of the planet B, which is cut by the plane 
in 3D space, perpendicular to line AB.


Again, the unseen part of the planet B from anythere of planet A is the hemi-sphere 
of B, cut from B by the great circle at B, which is in the perpendicular plane to line AB.


Same is true for the planet B: the unseen part of A from anythere on the B-surface is 
the "rear" hemi-sphere of A, in relation to the straigh line AB.


It is clear that these simple configurations of the unseen parts are due to the fact 
that the planets have the same radius.


    +------------------------------------------------------+
    |    We completed consideration of two planets and     |
    |       now we switch our focus to three planets.      |
    +------------------------------------------------------+


Let the planets be A, B and C, named according to their centers.

Whichever disposition of the centers A, B, C would be, their centers A, B and C form 
some plane in 3D space, and we will consider this plane, assuming that the three planets 
do not lie in the same straight line. Let "a", "b" and "c" be the interior angles 
of this triangle, opposite to the sides BC, AC, and AB, respectively.


The part of the planet C, unseen from both A and B, is the "rear" part of the C surface between
two planes: one plane is perpendicular to line AC and the other plane is perpendicular to line BC.


Since the angle between the lines AC and BC is "c", the angle between these two planes is 
(they are perpendicular to the lines AC and BC).

Therefore, the area of the C surface, which is unseen from A and B is   = .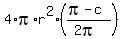


Similarly, the area of the B surface, which is unseen from A and C is   =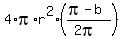 
and        the area of the A surface, which is unseen from B and C is   = .


To answer the problem question, we should add these three unseen areas, and we will get then


    total area of the three unseen regions =  =  = .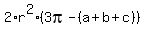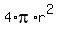


Notice that it is EXACTLY the surface area of one such sphere of the radius "r".


ANSWER.  Total area of the three unseen regions is .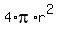


CHECK.   You can easily check the answer, by considering three spheres located in the vertices of the EQUILATERAL triangle.

         Then your common sense will tell you that the combined unseen area of the three spheres is exactly the surface area 
         of one such a sphere.