|
Question 1189158: A cylindrical can without a top is made to contain 75 in^3 of liquid. Find the dimensions that will minimize the cost of the metal to make the can.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A cylindrical can without a top is made to contain 75 in^3 of liquid.
Find the dimensions that will minimize the cost of the metal to make the can.
~~~~~~~~~~~~~~~~~~
The problem is to minimize the surface area of the described cylinder without the top.
As you know, the volume of a cylinder is
V =  ,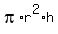
where pi = 3.14, r is the radius and h is the height.
In your case the volume is fixed:
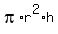= 75 cubic inches. (1)
The surface area of a top-opened cylinder is
S = 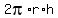 +  , (2)
and they ask you to find minimum of (2) under the restriction (1).
You can rewrite the formula (2) in the form
S(r) = 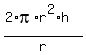 + . (3)
In formula (3), replace 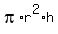by 75, based on (1). You will get
S(r) =  + =  + .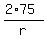
The plot below shows the function S(r) = + , and you can clearly see that it has the minimum.
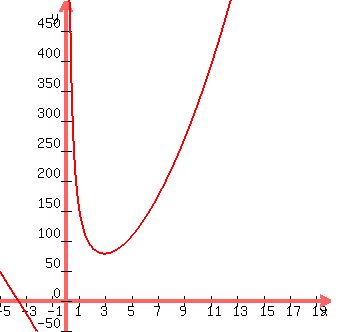Plot y = + 
To find the minimum, use Calculus: differentiate the function to get
S'(r) =  +  =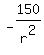 
and equate it to zero.
S'(r) = 0 leads you to equation  =  , which gives
r = 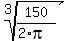 =  = 2.88 inches (approximately).
Answer. r = 2.88 inches, h =  = 2.88 inches give the minimum of the surface area.
Solved.
|
|
|
| |
