SOLUTION: On a sphere of diameter 125cm, two circles of the sphere whose planes are parallel have a radii 23cm and 53cm, respectively. Find the area of the zone included between these circle

Instead of doing it  for you, I'm going to show you how in detail:

  


We want the curved area on the outside of the flat-bottomed bowl
on the right, not including the area of its flat circular bottom.

The area of the outside of a FLAT-bottomed bowl (not including 
the flat bottom), cut from a sphere, is called a 'zone'.

The area of the outside of a ROUND-bottomed bowl, cut from a 
sphere, is called a 'cap'.

You can do this with calculus but there is a well-known formula 
for the area of the cap of a sphere. That formula is



The desired area is the difference between these two caps (round 
bottom bowls):



Now if we only had h, we could simply plug in the formula:



Here's how we find h.  We go back and draw lines up to the 
center of the sphere and a radius to an edge of the bowl.  Since 
the diameter of the sphere is given as 125, its radius is half of 
that or r=62.5.



Now you can finish.  Here's how:

1. Find the red line by the Pythagorean theorem.
2. Notice the red vertical line in the middle, which tells you 
that the vertical from the center of the sphere to the bottom 
of the bowl is also a radius and has length 62.5.
3. Subtract what you got from step 1 from the radius 62.5. That 
will give you the value of h.
4. Substitute in the formula: 

Now you finish on your own.

Edwin

When both parallel planes are on one side from the center of the sphere, then the distances 
to the planes from the center of the sphere are

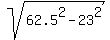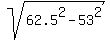     = 58.114 cm  (rounded)  and   = 31.125 cm  (rounded).


In this configuration, the distance between the planes is the difference 

    h = 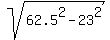 -  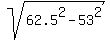= 58.114 - 31.125 = 24.989 cm  (rounded).


Then the area of the spherical zone between these two circles is

    A = 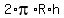 =  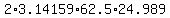= 9813.15 cm^2.




When the center of the sphere is BETWEEN the parallel planes, then the distances 
to the planes from the center of the sphere are the same

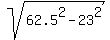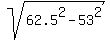     = 58.114 cm  (rounded)  and   = 31.125 cm  (rounded).


But in this configuration, the distance between the planes is the SUM 

    h = 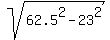 +  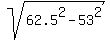= 58.114 + 31.125 = 89.239 cm  (rounded).


Then the area of the spherical zone between these two circles is

    A = A = 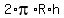 =  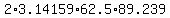= 35044.04375 cm^2.



Thus the problem has TWO answers:  9813.15 cm^2,  when the planes are on one side from the sphere center, 

                              and 35044.04 cm^2,  when the sphere center  is between the planes.

    Notice again, that the formula to calculate the surface area of the spherical zone remains the same in both cases


        A = ,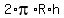


    but the values  " h "  of the zone height are DIFFERENT in each case.