|
Question 1172398: What is the volume of solid in xyz-space bounded by surfaces y = x^2, y = 2 - x^2, z = 0 and z = y + 3?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the volume of the solid.
**1. Determine the Region in the xy-Plane**
* We need to find the intersection of the parabolas y = x^2 and y = 2 - x^2.
* Set them equal: x^2 = 2 - x^2
* 2x^2 = 2
* x^2 = 1
* x = ±1
* When x = ±1, y = 1.
* The region in the xy-plane is bounded by these parabolas, with x ranging from -1 to 1.
**2. Set up the Triple Integral**
* The volume is given by the triple integral:
* V = ∫∫∫ dV
* The limits of integration are:
* z: 0 to y + 3
* y: x^2 to 2 - x^2
* x: -1 to 1
* The integral becomes:
* V = ∫(from -1 to 1) ∫(from x^2 to 2 - x^2) ∫(from 0 to y + 3) dz dy dx
**3. Evaluate the Integral**
* First, integrate with respect to z:
* ∫(from 0 to y + 3) dz = [z](from 0 to y + 3) = y + 3
* Now, integrate with respect to y:
* ∫(from x^2 to 2 - x^2) (y + 3) dy = [y^2/2 + 3y](from x^2 to 2 - x^2)
* = [(2 - x^2)^2/2 + 3(2 - x^2)] - [(x^2)^2/2 + 3(x^2)]
* = [4 - 4x^2 + x^4]/2 + 6 - 3x^2 - x^4/2 - 3x^2
* = 2 - 2x^2 + x^4/2 + 6 - 3x^2 - x^4/2 - 3x^2
* = 8 - 8x^2
* Finally, integrate with respect to x:
* ∫(from -1 to 1) (8 - 8x^2) dx = [8x - 8x^3/3](from -1 to 1)
* = [8(1) - 8(1)^3/3] - [8(-1) - 8(-1)^3/3]
* = [8 - 8/3] - [-8 + 8/3]
* = 8 - 8/3 + 8 - 8/3
* = 16 - 16/3
* = (48 - 16)/3
* = 32/3
**Answer**
The volume of the solid is 32/3 cubic units.
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the volume of solid in xyz-space bounded by surfaces y = x^2, y = 2 - x^2, z = 0 and z = y + 3?
~~~~~~~~~~~~~~~~~~~~~~
I will solve this problem mentally.
In (x,y)-plane, the area concluded between y = x^2, x-axis, and 0 <= x <= 1 is 1/3.
It is elementary calculation from Calculus.
From it, we deduce, that the area concluded between y = x^2, y = 1 and 0 <= x <= 1 is 2/3.
Hence, the area concluded between y = x^2 and y = 2-x^2 is 4 times 2/3, or 8/3 square units.
Now, our 3D solid consists of two parts.
One part is a right cylinder 0 <= z <= 3 over its base, which the area concluded
between y = x^2 and y = 2-x^2.
The volume of this cylinder is 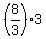 = 8 cubic units.
The other part is half of the cylinder 3 <= z <= 5 with the same base.
The height of this imaginary cylinder is 2 units (z from 3 to 5), so, its volume is = 8 cubic units.
The other part is half of the cylinder 3 <= z <= 5 with the same base.
The height of this imaginary cylinder is 2 units (z from 3 to 5), so, its volume is 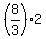 = 16/3.
The plane z = z + 3 cuts this cylinder in two parts of equal volumes - it is clear from the symmetry.
So, the whole volume of the 3D body under the interest is = 16/3.
The plane z = z + 3 cuts this cylinder in two parts of equal volumes - it is clear from the symmetry.
So, the whole volume of the 3D body under the interest is 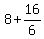 = = 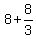 = = 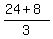 = 32/3 cubic units. = 32/3 cubic units.
Solved mentally.
My interior voice tells me that this mental solution
is what is expected in this problem.
|
|
|
| |