|
Question 114345: A NASA satellite makes a circular orbit around a planet of unknown diamter at an altitude of one mile above the planet.
Then NASA boosted the satellite to an altitude one mile higher(an altitude of two miles above planet.) In the second orbit, the satellite travels how many miles farther than it travelled on the first orbit?
(C=2pir)
>>>>>>>>>>>>PLEASE I NEED YOUR HELP.....THANKS IN ADVANCE
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A NASA satellite makes a circular orbit around a planet of unknown diamter at an altitude of one mile above the planet.
Then NASA boosted the satellite to an altitude one mile higher(an altitude of two miles above planet.) In the second orbit, the satellite travels how many miles farther than it travelled on the first orbit?
(C=2pir)
----------------
Lower orbit distance = 2(pi)(r+1) where r is the radius of the unknown planet.
-------------------
Upper orbit distance = 2(pi)(r+2)
-----------------
Difference EQUATION:
2(pi)(r+2)-2(pi)(r+1) = 2(pi)[(r+2)-(r+1)] = 2(pi) miles
==============
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You don't know the diameter of the planet, so let's call that  miles. The first orbit is one mile above the planet, so we know that the diameter of the orbit is miles. The first orbit is one mile above the planet, so we know that the diameter of the orbit is 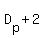 . We had to add 2 because 1 mile of altitude adds 1 mile to the radius, and the diameter is twice that. Now, if we move out to a point 2 miles above the surface, the diameter of the new orbit is . We had to add 2 because 1 mile of altitude adds 1 mile to the radius, and the diameter is twice that. Now, if we move out to a point 2 miles above the surface, the diameter of the new orbit is 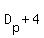 . .
We know that the distance travelled in the first orbit is the circumference of the circle with diameter 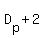 , or , or  , and the distance travelled in the second orbit is , and the distance travelled in the second orbit is  . .
Now we can subtract: 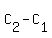 => => 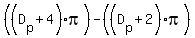 => => 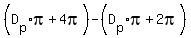 => =>  miles. Not too far, really, just a little over six and a quarter miles. miles. Not too far, really, just a little over six and a quarter miles.
Hope this helps,
John
|
|
|
| |