|
Question 1138930: Hello!
This is what I have given:
Regular Pyramid
LM = 5.2, m∠KFO = 35º
OF⊥ML, KF⊥ML
Find: V and Surface Area
Here is the image (copy paste into address bar)
https://homework.russianschool.com/resource?key=00st9
Thanks for helping!
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hey,
I know what RSM is: the Russian School of Math.
I know that the goal of RSM is to give an advanced Math education to their students, and the way to get this goal is in that
>>> the students solve their problems ON THEIR OWN. <<<
So, I have a question: did they at RSM instructed you to go the forum "algebra.com" with their problems
seeking for solutions from the outside ?
Did they allow you to go outside with their problems and to bring them back the solved problems - solved not by you,
but by others, and show these solutions as if it were you who solved them ?
Wouldn't it be across of their AND YOUR goals to go in this way ? ?? ???
Did they allow you to publish outside their intellectual property, in general ?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! from what i can determine, this is what happens.
you are given that ML is equal to 5.2.
since it is a square pyramid, then that means all the edges of the base are the same.
this means that PL, LM, MN, NP are all each equal to 5.2.
since this is a right pyramid, KO is vertical to the base and in the center of it.
this means that OF is half the length of an edge of the base of the pyramid.
that makes OF equal to 2.6 in length.
since angle KFO is 35 degrees and OF is equal to 2.6 in length, you can find the length of KO by using the trigonometric property of tan(KFO) = opposite / divided by adjaxcent = KO / 2.6.
you get tan(35) = KO / 2.6
solve for KO to get KO = 2.6 * tan(35) = 1.820539599.
use pythagorus theorem to get the length of KF = sqrt(KO^2 + OF^2) = 3.174013931.
you now have:
KO = 1.820539599
OF = 2.6
KF = 3.174013931
that's all in triangle KFO where KO is in the center of square PLNM and KF is in the center of LM and perpendicular to it.
you now turn your attentiojn to triangle KLM which is composed of two right triangle which are triangle KLF and KMF.
this is an isosceles triangle that has equal legs point to the vertex at angle LKM.
you know the length of KF and you know the length of LF.
LF is equal to half of LM which makes it equal to 2.6.
KF is what you just found from triangle KFO with a length of 3.174013931.
you can use this information to find the measure of angle KMF.
tan(KMF) = opposite / adjacent = KF / FM = 3.174013931 / 2.6 = 50.67731009 degrees.
the area of the base is equal to the square of one of the edges of the square.
this makes the area of the base equal to 5.2^2 = 27.04
the area of one of the triangles of the face of the pyramid is equal to 1/2 * the base * the height.
we'll use triangle34 KLM.
the area if 1/2 * the height of KF * the base of LM.
that would be 1/2 * 3.174013931 * 5.2 = 8.25243622.
there are 4 triangular faces and one square base to the surface area of the pyramid, so the surface area of the pyramids is equal to 4 * 8.25243622 + 27.84 = 60.04974488.
the volume of the pyramid is equal to 1/3 * the area of the base * the height.
that would be equal to 1/3 * 27.04 * 1.820539599 = 16.40913026.
that should be all that you were asked for, so i think we're done.
your solution would be, if i did this correctly:
surface rea = 60.04974488 square units.
volume = 16.40913026 cubic units.
i confirmed these measures are accurate through the use of an online square pyramid calculator that can be found at https://www.calculatorsoup.com/calculators/geometry-solids/pyramid.php
the display from the use of this calculator is shown below.
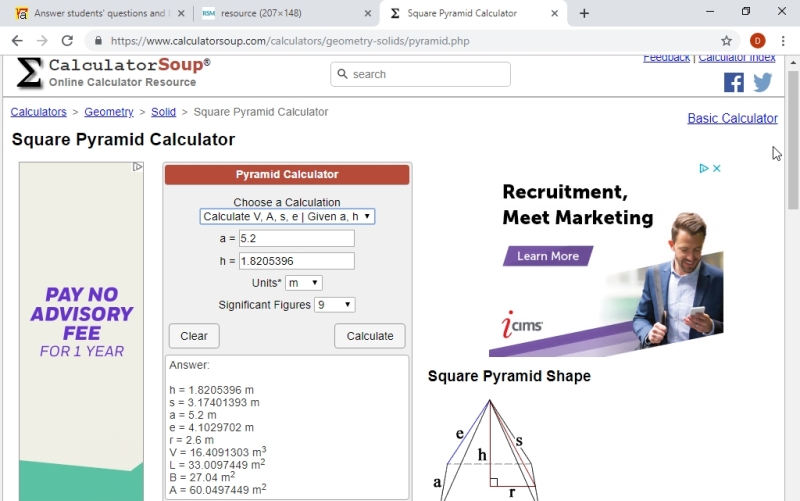
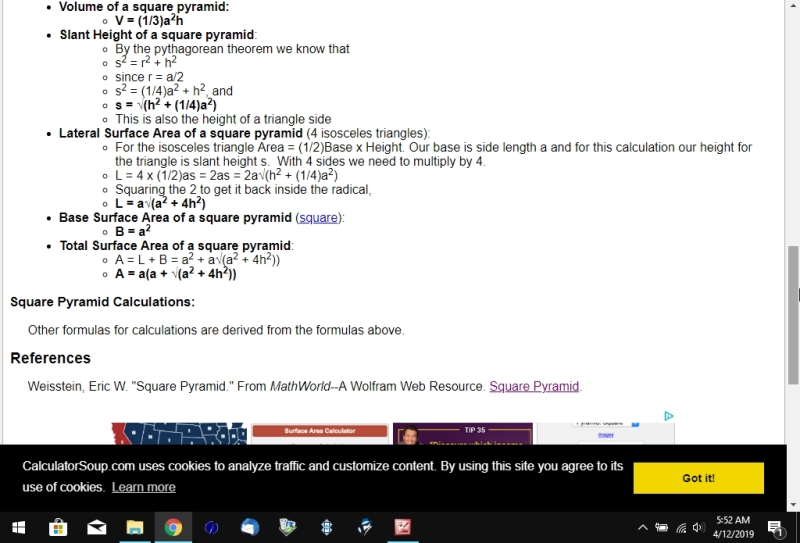
what i gave the calculator was the length of ML which was 5.2 and the height of the pyramid which was 1.820539599.
the calculator did the rest, confirming my other measurements as well as providing the surface area i calculated plus the volume i calculated.
|
|
|
| |