|
Question 1108960: A flower vase base radius 7cm height is 12cm slant height is 13cm. The flower vase has 500ml water .How much more water is equired to fill the flowet vase completely
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem suggests that the shape of the flower vase is a right cone frustum.
A cross section though the axis of that cone (with measurements in cm) would look like this:

Applying the Pythagorean theorem to the right triangle on the right side,





So the radius of the lower base (in cm) is  , ,
and the radius of the upper base of the cone frustum, in cm, is
 . .
If you are supposed to apply the formula
 to find the volume of the frustum, to find the volume of the frustum,
the volume of the vase, in cubic cm, is





Being reasonably accurate, we would say that the flower base can hold
 or or 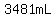 of water. of water.
Filling it to the brim, we could still add another
 . .
Without using a memorized formula, or an equivalent one
we would have to calculate the volume of the frustum as
the volume of a "parent" cone minus
the volume of another cone, cut off the parent cone's apex.
We would see that the shape of the vase is a frustum
cut from a "parent" cone with a base radius of 12cm,
and a height (in cm) of
 . .
The volume of such a parent cone (in cubic cm) would be
 , ,
and the cone cut off would have a height of
 . .
That height is  of the height of the larger cone, of the height of the larger cone,
so the cone cut off would have a volume
 times as large that of the parent cone. times as large that of the parent cone.
That would make the volume (in cubic cm) of the vase

|
|
|
| |