|
Question 1079788: A plane intersects only one nappe of a double-napped cone such that it is parallel to a generating line.
Which conic section is formed?
ellipse
parabola
hyperbola
circle
Found 2 solutions by Boreal, KMST:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! If it is parallel to the generating line, it will generate a circle. I am referring to the plane's passing parallel to the ends of both cones.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A parabola.
No need to memorize the answer.
A generating line for the cone
is a straight line on the cone's curved surface,
passing through the cone's apex.
In your mind, look from the side at an imaginary cone,
with a vertical axis,
and made of light colored glass.
The edges of the projection of the cone you see
look like two lines at an angle,
widening as you go away from the cone's apex.
The width of the intersection curve
goes fron nothing at the vertex of that intersection curve,
to the width of the cone at one point
(when the plane crosses the axis of the cone),
and then to less that the width of the cone.
That's what a parabola does.
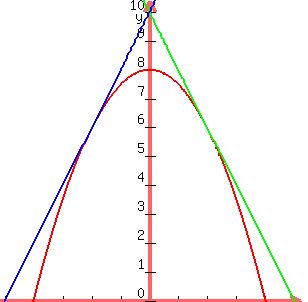
If the plane was parallel to the axis of the cone,
as the cone gets wider,
the intersection's curve's width would increase,
getting closer to the width of the cone,
but never quite reaching it.
That's a hyperbola and its asymptotes.
|
|
|
| |