In an examination Mr. X got a third of the answers wrong. In the same
examination Mr. Y got 5 of them wrong. Between both of them they answered
three quarters of the questions right. How many questions did Mr. X answer
correctly?
The number of questions is a multiple of 3
because Mr X got 1/3 of them wrong.
The number of questions is also a multiple
of 4 because together they got 3/4 of them
right.
Therefore the number of questions is a
multiple of 12, say 12k, where k is a
positive integer.
We use the "sieve" formula:
N(A or B) = N(A) + N(B) - N(A and B)
A = set of questions that Mr X got right
B = set of questions that Mr Y got right
Since Mr X missed 1/3 of the 12k, he got
2/3 of 12k right.
Since Mr Y missed 5 of the 12k, he got
12k-5 right
Since together they got 3/4 right, together
they got 3/4 of 12k right.
N(A) = 
= 8k
N(B) = 12k-5
N(A or B) = 
= 9k
Let p = N(A and B)
9k = 8k + 12k-5 - p
9k = 20k - 5 - p
p = 11k - 5 = the number that both got right.
The number that Mr X got right that Mr Y
missed = 8k-p = 8k-(11k-5) = -3k+5
That must not be negative. Therefore
-3k+5 ≥ 0
-3k ≥ -5
k ≤ 5/3
k ≤ 
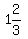k is a positive integer. Therefore k = 1,
and Mr X got 8k or 8(1) = 8 right.
-------------------------------------
There were 12 questions on the examination.
Mr X got 8 right and Mr Y got 7 right.
6 of them were right on both their exams.
Mr X got 2 right that Mr Y missed, and Mr Y
got 1 right that Mr X missed.
Their answer sheets probably looked like
this:
Mr X Mr Y
---- ----
1.√ 1.√
2.√ 2.√
3.√ 3.√
4.√ 4.√
5.√ 5.√
6.√ 6.√
7.√ 7.x
8.√ 8.x
9.x 9.√
10.x 10.x
11.x 11.x
12.x 12.x
Edwin
