SOLUTION: Please help. I need to graph this inequalities and fine the feasible region. The inequalities are; −3≤y≤5 4x+y≤5 −2x+y≤5. and says E = 4x - 3

Algebra ->  Average -> SOLUTION: Please help. I need to graph this inequalities and fine the feasible region. The inequalities are; −3≤y≤5 4x+y≤5 −2x+y≤5. and says E = 4x - 3      Log On


   

Question 810282: Please help. I need to graph this inequalities and fine the feasible region. The inequalities are; −3≤y≤5
4x+y≤5
−2x+y≤5.
and says E = 4x - 3y.
My teacher gets mad it homework is wrong but mainly if not done. Thanks.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I will show you how to graph those inequalities and find the feasible region first.
After that, I will tell you what I think of E+=+4x+-+3y .

THE FEASIBLE REGION:
The borders of your feasible region may be part of the lines
y=-3 , y=5 ,
4x%2By=5 , and
-2x%2By=5
Each of those lines is part of the solution to one of the inequalities.
The lines represented by y=-3 and y=5 are easy to figure out.
They are "horizontal" lines, where all the points have the same y-coordinate:
graph%28300%2C210%2C-10%2C10%2C-6%2C8%2C9%2C-3%2C5%29
The other two lines are slanted lines that are a little harder to figure out.
However, since two points determine a line, all we need is two find 2 points for each one.
Also, since they have to cross the horizontal lines y=-3 and y=5 ,
we might as well find the point where they cross y=-3 and y=5 .
To find each intersection point we solve a system of equations, but these are very simple.
Where does the horizontal line y=5 cross the slanted lines?
system%28y=5%2C4x%2By=5%29 --> 4x%2B5=5 --> 4x=0 --> x=0 gives us point {0,5) .
system%28y=5%2C-2x%2By=5%29 --> -2x%2B5=5 --> -2x=0 --> x=0 gives us point {0,5) too.
So, it turns out that the 3 lines represented by
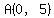y=5 , 4x%2By=5 , and -2x%2By=5 all cross at point A%280%2C5%29 .
Where does the horizontal line y=-3 cross the slanted lines?
system%28y=-3%2C4x%2By=5%29 --> 4x-3=5 --> 4x=3%2B5 --> 4x=8 --> x=8%2F4 --> x=2 gives us point B%282%2C-3%29 .
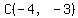system%28y=-3%2C-2x%2By=5%29 --> -2x-3=5 --> -2x=3%2B5 --> -2x=8 --> x=8%2F%28-2%29 --> x=-4 gives us point C%28-4%2C-3%29 .
Now we can mark those points and draw the slanted lines:
4x%2By=5 , passing through (0,5) and {2,-3) , and
-2x%2By=5 , passing through (0,5) and {-4,-3) .
Is triangle ABC the feasible region?
(Feasible regions are often polygons, like triangles, quadrilaterals, maybe even pentagons).
If triangle ABC is the feasible region, the origin, point O%280%2C0%29 should be a solution of all the inequalities.
-3%3C0%3C5 , 4%2A0%2B0=0%3C5 , and (((-2*0+0=0<5}}} ,
so point O%280%2C0%29 is a solution of all the inequalities.
For each of the 4 inequalities that determine the feasible region,
-3%3C=y, y%3C=5, 4x%2By=5 , and -2x%2By=5 ,
the solution is the corresponding boundary line, plus the whole side of the line that contains the origin, point O%280%2C0%29 .
So the points that satisfy all 4 inequalities are the points in triangle ABC, including the sides of the triangle.

WHAT ABOUT E+=+4x+-+3y ?
Usually you are asked to find out where in the feasible region the function E has a maximum or minimum value.
(E is a linear function of x and y).
For a linear function in a polygon-shaped feasible region,
the maximum must happen in one of the vertices or all along one tof the sides/edges of the feasible region.
The sames goes for the minimum.
All we have to do is calculate the value of E at points A, B, and C
At 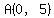A%280%2C5%29 ,
E=4%2A0-3%2A5=-15
At B%282%2C-3%29 ,
E=4%2A2-3%2A%28-3%29=8%2B9=17
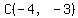At C%28-4%2C-3%29 ,
E=4%2A%28-4%29-3%2A%28-3%29=-16%2B9=-7
So the maximum of E happens at B%282%2C-3%29 , where E=17 ,
and the minimum happens at 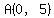A%280%2C5%29 , where E=-15 .