SOLUTION: Given f(x) = -4x + 1, A. Find the average rate of change from 2 to 5. B. Find an equation of the secant line containing (2, f(2)) and (5, f(5)).

As x goes from 2 to 5, y [or f(x)] goes from f(2)=-4(2)+1=-7 to f(5)=-4(5)+1=-19

From -7 to -19 is a change of (-19)-(-7)=-19+7=-12 in y

From 2 to 5 is a change of 5-2 = +3 in x

So the average change in y [or f(x)] per the average change in x
is -12 units change in y per a +3 change in x, which means an average
change of (-12)/(+3)=-4 y-units change per x-units change.

That's what the slope is, the change in y, divided by the change in x 

Answer: -4 change in f(x) y-units per x-unit change.

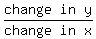
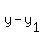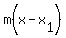
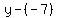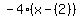
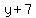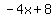
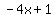change y to f(x)



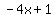So the secant line coincides with the graph of f(x).

[That happens when the graph of the given function 
f(x), is a line, but not when the given function curves].

Here is a case when the given function f(x) curves, and
the secant line does not coincide with the given function f(x)



The black line is the secant line. It only has two points
in common with the function f(x) (the red curve).

But your problem here is not a curve: 

The case you were given was a special case when the 
secant line happens to coincide with the function f(x),
like what you see below, where the black line, which is 
the secant line, coincides with the red line, which is the 
graph of f(x).

Your teacher gave you a very special case, but most graphs
for f(x) are not straight lines, and the secant lines
will usually have only two points in common with the graph
of the given function f(x) like the graph above.

Remember what the word "secant" means, a line that cuts
through a curve, as you see in the first curve.  

[Remember from your geometry that a secant line was a line
that cuts through a circle.] 

Your problem here is a special case when the secant line
doesn't "cut through" the curve of f(x) but coincides with it. 



This type problem is to prepare you for calculus, where
you will learn about the secant line approaching a tangent
line.  You will also remember from your geometry that a
tangent line just touches a circle in one point, and does
not cut through the circle.  I didn't want you to get
confused because your teacher gave you such a special case.
Just remember that most of your problems will be like the
curve in the first graph above, not the lower special case,
which you were given.

Edwin