Question 1204664: a nurse wants to make 50 ml of a 20% morphine solution. she needs to mix 10% morphine solution with 50% morphine solution to make this happen. how many ml of each must she mix?
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
a nurse wants to make 50 ml of a 20% morphine solution.
she needs to mix 10% morphine solution with 50% morphine solution to make this happen.
how many ml of each must she mix?
~~~~~~~~~~~~~~~~~~~
Let x be the the volume of the 50% morphine solution to use, in milliliters.
Then the volume of the 10% solutions of morphine is (50-x) mL,
to make the total volume of 50 mL.
The 50% solution contributes 0.5x mL of the pure morphine to the final mixture.
The 10% solution contributes 0.1*(50-x) mL of the pure morphine to the final mixture.
So, the total amount of the pure morphine in 50 Ml of the final mixture is
0.5x + 0.1*(50-x) milliliters.
We want this amount of the pure morphine provides 20% final solution.
So, we write this equation, which describes it
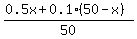 = 0.2.
Simplify it by multiplying both sides by 50
0.5x + 0.1*(50-x) = 0.2*50.
Simplify further and express x
0.5x + 5 - 0.1x = 10
0.5x - 0.1x = 10 - 5
0.4x = 5
x = 5/0.4 = 12.5.
ANSWER. 12.5 mL of the 50% morphine solution and 50-12.5 = 37.5 ml of the 10% morhine solution should be used.
CHECK. 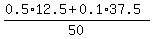 = 0.2, or 20% concentration of the final solution. ! correct !
Solved.
-----------------
It is a standard and typical mixture problem.
For introductory lessons covering various types of mixture word problems see
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Batch A: 10% morphine
Batch B: 50% morphine
Target concentration: 20% morphine
The gap from 10% to 20% is 10
The gap from 20% to 50% is 30
The ratio 10:30 reduces to 1:3
The nurse will need 3 times as much of one solution compared to the other.
The ratio 1:3 scales up to 1x:3x for some positive real number x.
Add up those parts and set the sum equal to the goal of 50 mL.
1x+3x = 50
4x = 50
x = 50/4
x = 12.5
She'll need x = 12.5 mL of one batch and 3x = 3*12.5 = 37.5 mL of the other batch.
The question is: which values go where?
Let's make a table where we have 12.5 mL of batch A and 37.5 mL of batch B
| Amount of solution | Amount of pure morphine | | A | 12.5 | 0.10*12.5 = 1.25 | | B | 37.5 | 0.50*37.5 = 18.75 | | Total | 50 | 1.25+18.75 = 20 |
The takeaway from that table is we have 20 mL of pure morphine out of 50 mL total
20/50 = 0.40 = 40% is the final concentration.
We wanted a 20% concentration instead, so we must flip the values.
| Amount of solution | Amount of pure morphine | | A | 37.5 | 0.10*37.5 = 3.75 | | B | 12.5 | 0.50*12.5 = 6.25 | | Total | 50 | 3.75+6.25 = 10 |
10 mL of pure morphine out of 50 mL total
10/50 = 0.20 = 20% is the final concentration, which is the target we're after.
Answers:
37.5 mL of the 10% solution
12.5 mL of the 50% solution
More practice with a similar question
https://www.algebra.com/algebra/homework/word/mixtures/Mixture_Word_Problems.faq.question.1204463.html
|
|
|
