Question 1066073: how many whole number solutions are there to the question...
The average of three whole numbers is 15.
1a What could the three numbers be?
1b How many triplets are there?
1c How do you know that you have got them all?
(a+b+c)/3=15
I have lots but know there must be an easier way to find the answer
so a+b+c=45 therefore many answers starting with
0+0+45=45 therefore a=0 b=0 and c=45
0+1+44 =45 therefore a=0 b=1 and c=44
0+2+43 +45 therefore a=0 b=2 and c=43...etc
1b i think there is only one triplet 15, 15 , 15 ie each number is 15. presuming that is what is meant by the term 'triplet'
1c think there must be a formula for this. or is it simply 45+45+45, total 135 different solutions (from counting up all the different combinations above).
with thanks from a middle aged student attempting to re learn stuff!
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
If the average of three whole numbers is 15, then the sum is 45.
In opposite, if the sum of three whole numbers is 45, then the average is 15.
So, the average is 15 if and only if the sum is 45.
So, your question has other equivalent formulation:
How many are there triplets (a,b,c) of whole numbers with the sum a + b + c = 45 ?
1. Let a = 0.
Then any pair (b,c) works if b + c = 45.
You can take b = 0, 1, 2, . . . , 44, 45 and then adjust c.
In all, there are 46 such pairs.
In other words, there are 46 triples of the form (0, b, c).
2. Let a = 1.
Then any pair (b,c) works if b + c = 45-1 = 44.
You can take b = 0, 1, 2, . . . , 44 and then adjust c.
In all, there are 45 such pairs.
In other words, there are 45 triples of the form (1, b, c).
3. Let a = 2.
Then any pair (b,c) works if b + c = 45-2 = 43.
You can take b = 0, 1, 2, . . . , 43 and then adjust c.
In all, there are 44 such pairs.
In other words, there are 44 triples of the form (2, b, c).
. . . .
By continuing this way, you find that the number of triples is
46 + 45 + 44 + . . . + 1.
This last "1" corresponds to the case a = 45, when for "a" and "b" you have the only choice a= 0 and b= 0.
Now, the sum 46 + 45 + 44 + . . . + 1 =  .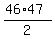
It is the sum of the first 46 positive integers.
So, your answer is 23*47 = 1081 triples.
For the sum of the first "n" positive integers see the lessons
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
|
|
|
