Question 891836: Provided AB has length 5 cm, BC has length 3 cm, and the measurement of angle A is 30 degrees, draw triangle ABC, and describe why these conditions do not determine a unique triangle. I'll try to draw the shape, but I don't know how to describe why the conditions don't determine a unique triangle. I've been stuck on these problems for a week now. They're actually due next week, but I don't want to try it at the last minute.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website! Provided AB has length 5 cm, BC has length 3 cm, and the measurement of angle A is 30 degrees, draw triangle ABC, and describe why these conditions do not determine a unique triangle. I'll try to draw the shape, but I don't know how to describe why the conditions don't determine a unique triangle. I've been stuck on these problems for a week now. They're actually due next week, but I don't want to try it at the last minute.
Since we’re given 2 sides and a NON-INCLUSIVE angle, we need to use the Law of Sines to determine
how many distinct triangles can be formed. If more than one (1) triangle can be formed from the
given measurements, then the triangle is NOT UNIQUE, or NOT DISTINCT.
Since side BC is opposite angle A, then side BC = a = 3
Also, since side AB is opposite angle C, then side AB = c = 5
Using the law of sines, we get: 
 ------ Substituting angle A, and sides a & c to determine angle C ------ Substituting angle A, and sides a & c to determine angle C
 ------ Cross-multiplying ------ Cross-multiplying

sin C = .833333
Angle C = 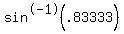 = = 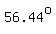 ≈ ≈ 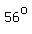
This means that the 3rd angle, or angle B = 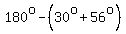 , or , or 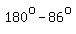 , or , or 
Now, the reference angle of angle C is in the 2nd quadrant, and is: 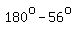 , or , or 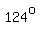 . .
Now, with angle A being  , and the reference angle of angle C being , and the reference angle of angle C being 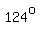 , a 2nd triangle, , a 2nd triangle,
with an angle measurement of B = 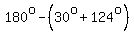 , or B = , or B = 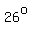 CAN BE FORMED. CAN BE FORMED.
Therefore, the given triangle with the given measurements represents a NON-DISTINCT or
NON-UNIQUE triangle, since 2 triangles: one measuring:
 , , 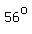 , and , and  , and another measuring: , and another measuring:
 , , 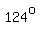 , and , and 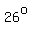 , can be formed. , can be formed.
|
|
|