|
Question 1204564: point P is not on line AB. line BV and FG both run through P and line AB. what can you conclude about line BV and line FG.
A. BV and FG cannot both be perpendicular to AB
B.BV and FG are congruent lines
C. BV and FG are perpendicular to each other
D.BV and FG are both perpendicular to AB
E.BV and FG intersect AB at the same point
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's Assume That The Given Line is  , and the point is , and the point is  , which is not on , which is not on  . .
Now, Let's assume, We have drawn a perpendicular 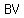 on on  , and intersecting line , and intersecting line  at a point at a point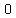 . .
We have to prove that, this 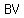 is the is the  line passing through line passing through  that is that is  to to  . .
Now, we will use a construction.

Let's construct another perpendicular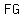 on on  from point from point  . .
Proof:
We have,
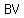 perpendicular perpendicular  . .
Also, 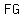 perpendicular perpendicular  . .
So, 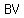 || || 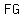 . [Both are perpendiculars on the same line.] . [Both are perpendiculars on the same line.]
Now since both 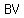 and and 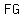 have point have point 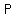 . .
So, 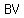 and and 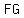 are the coincident lines or parallel lines and only one of them passes through point a are the coincident lines or parallel lines and only one of them passes through point a } }
answer:
A.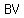 and and 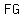 cannot both be perpendicular to cannot both be perpendicular to 
Answer by greenestamps(13223)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is not sufficient to get a single answer from among the answer choices.
Choice B makes no sense and so can't be a right answer; lines are infinite in length and can't be congruent.
Choice C is not right. You can certainly make BV and FG perpendicular, but that will be a very special case.
Now what about choices D and E....
If two lines are perpendicular to a given line and both pass through a point P not on that line, then the two lines are the same line, and they will intersect the line at the same point.
And there is nothing in the statement of the problem that says BV and FG can't be the same line.
So answer choices D and E are both possible in one special case, but they are not true in the general case.
And answer choice A is not true in the special case where BV and FG are the same line.
So, because the statement of the problem does not specify that BV and FG are not the same line, none of the conclusions A to E is possible.
|
|
|
| |