|
Question 1074041: Please answer this is really hard. The observed angles of a quadrilateral after station and side adjusmtments are: Angle DBA=30 Degrees angle CBD=48 Degrees angle BCA=59 Degrees and angle DCA =21 degrees. Compute the angles BDA,DAC and DAB
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I do not know what was meant by "station and side adjustments."
I imagine the quadrilateral (with its diagonals) looks like this,
 or a rotated and/or flipped version. or a rotated and/or flipped version.
 , ,  , ,  , and , and  . .
So,  and and 
Also,  and and
 based on the sum of angle measures for triangles BXC and BAC respectively. based on the sum of angle measures for triangles BXC and BAC respectively.
With that, I can compute approximate measures for BDA, DAC and DAB.
It takes quite a bit of coordinate geometry calculations, and I do not get an exact value, but it is the best I can do so far.
For ease of calculations, I set coordinates for points C and B as
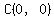 and and 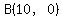 . .
Then I find coordinates for  and and 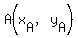 . .
 --> -->  --> -->  --> --> 
Approximate value: 
Similarly for A,

Approximate value: 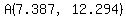 . .
(I have my computer keep more digits in these calculations, because they are intermediate calculations, and I round at the end).
The slope of line DA is the tangent of the angle DA makes with the x-axis (or with any horizontal line).
It is  . .
That is the tangent of approximately a  angle. angle.
Since line BD makes a 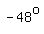 angle with the horizontal, angle with the horizontal,
the measure of angle BDA is about  . .
 based on the angles DA and AC make with the x-axis. based on the angles DA and AC make with the x-axis.
Or,  based on the sum of angle measures for triangle ADX. based on the sum of angle measures for triangle ADX.
Finally,  . .
|
|
|
| |