y = -x^2+3x-4
compare to:
y = ax^2+bx+c
a=-1, b=3, c=-4
1. It has an x^2 term, so the graph of the equation is a parabola.
2. The coefficient of the x^2 term, a=-1, is negative so the parabola opens downward.
3. The constant term c is -4, so the y-intercept is (0,c) = (0,-4).
4. To find the vertex we use the vertex formula for the x-coordinate of the vertex,
which is 
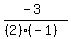
, that also tells us that the line of symmetry
has equation 
5. The y-coordinate of the vertex is found by substituting the x-coordinate
of the vertex, h, for x in the original equation:
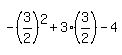
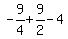
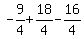
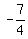6. The vertex is below the x-axis and the parabola opens downward so there
are no x-intercepts, and there is no use to try to find any.
7. The vertex is the point (h,k) =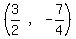 
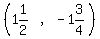8. We plot the vertex, the y-axis and the line of symmetry (in green):
9. Using the line of symmetry, we find the point symmetrical to the y-intercept,
which is (3,-4) on the other side of the line of symmetry:
10. And now it's easy to sketch in the parabola:
Edwin
