Determine the value(s) of for which the following system of equations has
nontrivial solutions.
(k+4)x + (k-2)y = 0
4x + (k-3)y = 0
Please explain how you get the answer so I can do the others.
"Non-trivial" means other than (x,y) = (0,0)
= 
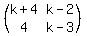
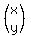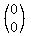If the coefficient matrix 
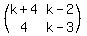has an inverse, we could left-multiply both sides by that inverse and
there could only be the trivial solution. That's because that inverse
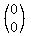times on the right could only give 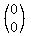on the right
So there could only be a nontrivial solution if the coefficient matrix
is singular (has no inverse). This only occurs when its
determinant is 0. (That is, when Cramer's rule fails).
Thus we set its determinant = 0
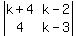= 0
(k+4)(k-3) - 4(k-2) = 0
Multiply that out, solve it and get two solutions
k = -1 and k = 4
Using k = -1,
(-1+4)x + (-1-2)y = 0
4x + (-1-3)y = 0
3x - 3y = 0
4x - 4y = 0
Both those are equivalent to y = x, so when k = -1,
then there are infinitely many solutions, and they
all have the form (c,c) where c is any number.
Using k = 4,
(4+4)x + (4-2)y = 0
4x + (4-3)y = 0
8x - 2y = 0
4x - y = 0
Both those are equivalent to y = 4x, so when k = 4,
then there are infinitely many solutions, and they
all have the form (c,4c) where c is any number.
Edwin
