Question 80816: This is a question from a class homework assignment.
Given a line containing the points (1,3), (2,4), (3,5) determine the slope-intercept form of the equation, give one additional point on this line and graph function.
Equation of line in slope-intercept form:
show your work:
Give one additional point in (x,y) form that would fall on this line:
Graph the function:
Answer by funmath(2933)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given a line containing the points (1,3), (2,4), (3,5) determine the slope-intercept form of the equation, give one additional point on this line and graph function.
Equation of line in slope-intercept form:
show your work:
Use the slope formula to find the slope of the line:
 (x1,y1)=(1,3) (x2,y2)=(2,4) (x1,y1)=(1,3) (x2,y2)=(2,4)



Use the point slope formula to find the equation of the line:
 m=1 (x1,y1)=(1,3) m=1 (x1,y1)=(1,3)




Check to make sure that the third point (3,5) is part of the line.


Ok, so all three points are colinear and the equation of their line is:

Give one additional point in (x,y) form that would fall on this line:
Let x be anything, 0 hasn't been used yet.


Another point on the line would be: (0,2)
Graph the function:
Plot the points and connect them and you'll have the following line:
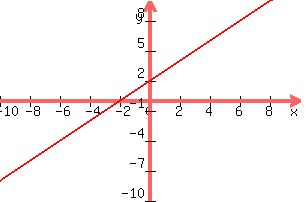
Happy Calculating!!!!
|
|
|