Question 741884: I am trying to solve a lesson example in my algebra 2 textbook. I don't understand the graph they used for the solution. Here is the question:
Gillian is planning a green roof that will cover up to 600 square feet. She will use two types of plants: blue lagoon sedum and raspberry red sedum. Each blue lagoon sedum will cover 1.2 square feet. Each raspberry red sedum will cover 2 square feet. Each plant costs $2.50, and Gillian must spend less than $1000. Write the constraints, and graph the feasible region.
x = # of blue lagoon sedums
y = # of raspberry red sedums
The book uses the equations:
x >= 0
y >= 0
1.2x + 2y <= 600
2.50x + 2.50y <= 1000
I solved 1.2x + 2y <= 600 for y. I got y >= -0.66 + 300.
When I solve 2.50x + 2.50y <= 1000 for y I get x >= y + 400 (by replacing y with -0.66 + 300).
The graph in the book shows 300 as the y intercept and 400 as the x intercept. If they are using y = mx + b format, I don't know if I should have solved 2.50x + 2.50y <= 1000 for y or x. Whether I solve for x or y I still come out with a y intercept of 400. What am I doing wrong?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Very often you do not have to solve for x or y.
Your boundary lines will be straight lines, and to graph each line, you will need at most 2 points. Finding and plotting those 2 points may be easier than you think.
The book uses
 because the number for x cannot be negative because the number for x cannot be negative
 because the number for y cannot be negative because the number for y cannot be negative
Those are two of the constraint.
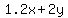 is the surface area that the plants will cover, in square feet, which could be up to 600 square feet. That gives you the inequality is the surface area that the plants will cover, in square feet, which could be up to 600 square feet. That gives you the inequality

The total cost, in $, will be 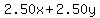 and must not be more than $1000, and that gives you the inequality and must not be more than $1000, and that gives you the inequality

THE BOUNDARIES OF THE FEASIBLE REGION:
 and and  are the y an x axes respectively (no calculations needed to graph those lines), and the space where are the y an x axes respectively (no calculations needed to graph those lines), and the space where  and and  is the first quadrant including the pieces of the axes that border the quadrant. is the first quadrant including the pieces of the axes that border the quadrant.
The boundary line  is a straight line that passes through A(0,300) and P(500,0) is a straight line that passes through A(0,300) and P(500,0)
because  means means  --> -->  --> -->  and and
 means means  --> -->  --> --> 
Another boundary is  --> -->  (dividing everything by 2.50). (dividing everything by 2.50).
Making  first and then first and then  (as for the other line), you can easily find that (as for the other line), you can easily find that  passes through Q(0,400) and C(400,0). passes through Q(0,400) and C(400,0).
The graph of the boundaries looks like this:
 The feasible region is the quadrilateral ABCO. The feasible region is the quadrilateral ABCO.
How do we know that the feasible region is the part below both slanted lines?
We know that
 (line AP), and (line AP), and
 (line QC) are boundary lines. (line QC) are boundary lines.
For  the boundary line is the boundary line is  . .
The points to one side of that line have 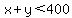 , and the points to the other side have , and the points to the other side have 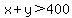 . .
What side satisfies 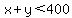 ? ?
We can check with a test point that is not on the boundary line.
An easy choice for a test point is O(0,0). Is it part of the solution to  ? ?
When  and and  , ,  , so O(0,0) satisfies , so O(0,0) satisfies 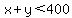 and so do all the points on the same side of QC. and so do all the points on the same side of QC.
Similarly, you can find that the side of  that is the solution you that is the solution you  is the side that contains O(0,0). is the side that contains O(0,0).
The only hard-work calculation you could have to do is finding the coordinates of point B, if you need to, but you may not be expected to do that for this problem.
If you had to, the coordinates of point B are the solution to
 . .
NOTE:
You may think that you have to solve for y to get
 --> -->  to figure out that the points that satisfy to figure out that the points that satisfy
 are those below the line are those below the line  <--> <-->  but you do not need to do that much work (unless your teacher wants you to do it that way). but you do not need to do that much work (unless your teacher wants you to do it that way).
|
|
|