Question 460760: Show that if s=(v1,v2,v3) is a linearly dependent set of vectors in a vector space V, and v4 is any vector in V that is not in S, then {v1,v2,v3,v4} is also linearly dependent
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let S = { 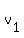 , , 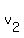 , , 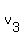 } be a linearly dependent set of vectors in V. } be a linearly dependent set of vectors in V.
This means that there are scalars 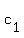 , ,  , and , and 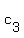 , not all of them zero, such that , not all of them zero, such that  . But then, we would also have . But then, we would also have  , letting , letting  ; and not all of ; and not all of 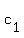 , ,  , , 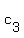 , and , and 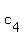 are equal to zero. Hence { are equal to zero. Hence { 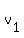 , , 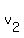 , , 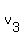 , , 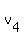 } is also a linearly dependent set. } is also a linearly dependent set.
|
|
|